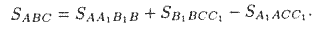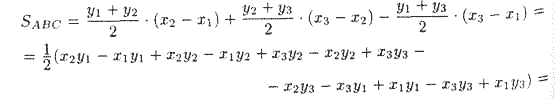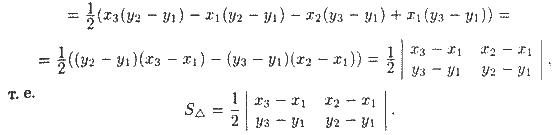Основные приложения метода координат на плоскости.
Расстояние между двумя точками:
Деление отрезков в данном отношение: Введем в рассмотрение векторы и. Точка Μ делит отрезок АВ в отношении λ, если
но
Учитывая, что равные векторы имеют равные координаты, получаем
Формулы (9.2) и (9.3) называются формулами деления отрезка в данном отношении. В частности, при λ = 1, т.е. если AM = MB, то они примут вид
Замечание: Если λ = 0, то это означает, что точки A и Μ совпадают, если λ < 0, то точка Μ лежит вне отрезка АВ — говорят, что точка M делит отрезок АВ внешним образом ( Площадь треугольника: Опустим из вершин А, В, С перпендикуляры АА1, ВВ1, СС1 на ось Ох Очевидно, что Поэтому
Замечание: Если при вычислении площади треугольника получим S = 0, то это означает, что точки А, В, С лежат на одной прямой, если же получим отрицательное число, то следует взять его модуль.
|

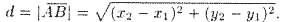
 (9.1)
(9.1)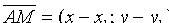 , т.е.
, т.е.  и
и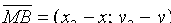 , т.е.
, т.е. 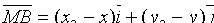


 ,
,  В этом случае точка М(х;у) является серединой отрезка АВ.
В этом случае точка М(х;у) является серединой отрезка АВ.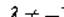 т. к. в противном случае
т. к. в противном случае 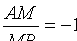 , т. е. AM + MB = 0, т. е. АВ = 0).
, т. е. AM + MB = 0, т. е. АВ = 0).