Полярное, нормальное уравнение прямой.
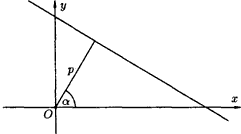
Найдем уравнение прямой в полярных координатах. Ее положение можно определить, указав расстояние р от полюса О до данной прямой и угол а между полярной осью ОР и осью l, проходящей через полюс О перпендикулярно данной прямой (см. рис.22). Для любой точки М(г; j) на данной прямой имеем:
С другой стороны,
Следовательно,
Полученное уравнение (13) и есть уравнение прямой в полярных координатах. Пусть прямая определяется заданием р и a (см. рис. 45). Рассмотрим прямоугольную систему координат Оху. Введем полярную систему, взяв О за полюс и Ох за полярную ось. Уравнение прямой можно записать в виде
Но, в силу формул, связывающих прямоугольные и полярные координаты, имеем: r cos j = x, r sin j = у. Следовательно, уравнение (13) прямой в прямоугольной системе координат примет вид
Уравнение (14) называется нормальным уравнением прямой.
Умножим все члены уравнения (7) на некоторый множитель l А = cos a, l В = sin a, l С = - р. Из первых двух равенств находим l 2 А2 + l 2 В2 = cos2 a + sin2 a, т. е. l С = - р знак нормирующего множителя противоположен знаку свободного члена С общего уравнения прямой.
|
(13)
т.е. 
(14)
Покажем, как привести уравнение (7) прямой к виду (14).
. Получим l Ах + l Ву + l С = 0. Это уравнение должно обратиться в уравнение (14). Следовательно, должны выполняться равенства:
. Множитель l называется нормирующим множителем. Согласно третьему равенству
