Перпендикулярности плоскостей.
Если две плоскости (α1 и α2) заданы общими уравнениями вида: A1x+B1y+C1z+D1 =0 и A2x+B2y+C2z+D2 =0, то очевидно, что угол между ними равен углу между их нормалями, то есть между векторами n 1={ A1,B1,C1) и n 2={ A2,B2,C2). Из формулы (5.6) получаем, что косинус угла между плоскостями α1 и α2 равен Условие параллельности плоскостей заключается в параллельности нормалей: а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения: A1A2 + B1B2 + C1C2 = 0. (8.6)
Выведем еще несколько уравнений плоскости. Пусть плоскость проходит через точки М 1(х1, у1, z1), M 2(x2, y2, z2) и M 3(x3, y3, z3), не лежащие на одной прямой. Тогда векторы М1М 2 ={ x2 - x1, y2 - y1, z2 - z1 }, М1М 3 ={ x3 - x1, y3 - y1, z3 - z1 }и М1М ={ x - x1,y - y1, z - z1 }, где М(x, y, z) – произвольная точка плоскости, компланарны. Следовательно, их смешанное произведение равно нулю. Используя координатную запись смешанного произведения, получаем: Это уравнение, которому удовлетворяют координаты х, у, z любой точки, лежащей на искомой плоскости, является уравнением плоскости, проходящей через три данные точки. Способом, аналогичным изложенному в лекции 7, можно получить нормальное уравнение плоскости: где р – длина перпендикуляра ОР, опущенного из начала координат на плоскость, а cosα, cosβ, cosγ – направляющие косинусы нормали к этой плоскости. При этом расстояние от любой точки А пространства до данной плоскости определяется по формуле: где x0,y0,z0 – координаты рассматриваемой точки А. Подмодульное выражение в формуле (8.9) называется отклонением точки А от плоскости и принимает положительные значения, если А и начало координат лежат по разные стороны от плоскости, и отрицательные, если эти две точки лежат по одну сторону от плоскости. Нормальное уравнение получается из общего уравнения плоскости в результате деления его на нормирующий множитель Доказательства всех сформулированных утверждений полностью аналогичны исследованию нормального уравнения прямой на плоскости, рассмотренного в лекции 7.
|

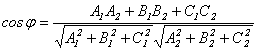 (8.4)
(8.4) (8.5)
(8.5)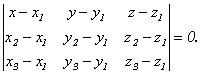 (8.7)
(8.7)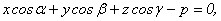 (8.8)
(8.8) , (8.9)
, (8.9) знак которого противоположен знаку D.
знак которого противоположен знаку D.


