Угол между прямыми. Угол между прямой и плоскостью.
Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида Условия параллельности и перпендикулярности прямых тоже сводятся к соответствующим условиям для их направляющих векторов: Угол φ между прямой, заданной каноническими уравнениями Ax + By + Cz + D = 0, можно рассматривать как дополнительный к углу ψ между направляющим вектором прямой и нормалью к плоскости. Тогда Условием параллельности прямой и плоскости является при этом условие перпендикулярности векторов n и а: Al + Bm + Cn = 0, (8.18) а условием перпендикулярности прямой и плоскости – условие параллельности этих векторов: A/l = B/m = C/n. Пример 1.15. Cоставьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости. Решение. По условию задачи вектор ОА (1,-1,3) является нормальным вектором плоскости, тогда ее уравнение можно записать в виде Пример 1.16. Составьте уравнение плоскости, проходящей через ось Оz и образующей с плоскостью 2x+y- Решение. Плоскость, проходящая через ось Oz, задается уравнением Ax+By=0, где А и В одновременно не обращаются в нуль. Пусть В не Решая квадратное уравнение 3m 2 + 8m - 3 = 0, находим его корни Пример 1.17. Составьте канонические уравнения прямой: Решение. Канонические уравнения прямой имеют вид: где m, n, р - координаты направляющего вектора прямой, x 1, y 1, z 1 - координаты какой-либо точки, принадлежащей прямой. Прямая задана как линия пересечения двух плоскостей. Чтобы найти точку, принадлежащую прямой, фиксируют одну из координат (проще всего положить, например, x=0) и полученную систему решают как систему линейных уравнений с двумя неизвестными. Итак, пусть x=0, тогда y + z = 0, 3y - 2z+ 5 = 0, откуда y=-1, z=1. Координаты точки М(x 1, y 1, z 1), принадлежащей данной прямой, мы нашли: M (0,-1,1). Направляющий вектор прямой легко найти, зная нормальные векторы исходных плоскостей n 1 (5,1,1) и n 2 (2,3,-2). Тогда
Канонические уравнения прямой имеют вид: x/(-5) = (y + 1)/12 = Пример 1.18. В пучке, определяемом плоскостями 2х-у+5z-3=0 и х+у+2z+1=0, найти две перпендикулярные плоскости, одна из которых проходит через точку М(1,0,1). Решение. Уравнение пучка, определяемого данными плоскостями, имеет вид u(2х-у+5z-3) + v(х+у+2z+1)=0, где u и v не обращаются в нуль одновременно. Перепишем уравнение пучка следующим образом: (2u +v)x + (- u + v)y + (5u +2v)z - 3u + v = 0. Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим: (2u+v) × 1 + (-u + v) × 0 + (5u + 2v) × 1 -3u + v =0, или v = - u. Тогда уравнение плоскости, содержащей M, найдем, подставив v = - u в уравнение пучка: u(2x-y +5z - 3) - u (x + y +2z +1) = 0. Т.к. u ¹ 0 (иначе v=0, а это противоречит определению пучка), то имеем уравнение плоскости x-2y+3z-4=0. Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности плоскостей: (2u+ v) × 1 + (v - u) × (-2) + (5u +2v) × 3 = 0, или v = - 19/5u. Значит, уравнение второй плоскости имеет вид: u(2x -y+5z - 3) - 19/5 u(x + y +2z +1) = 0 или 9x +24y + 13z + 34 = 0.
|

 и
и  косинус угла между ними можно найти по формуле:
косинус угла между ними можно найти по формуле: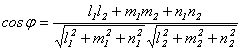 . (8.14)
. (8.14) - условие параллельности прямых, (8.15)
- условие параллельности прямых, (8.15) - условие перпендикулярности прямых. (8.16)
- условие перпендикулярности прямых. (8.16)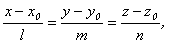 и плоскостью, определяемой общим уравнением
и плоскостью, определяемой общим уравнением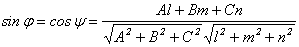 (8.17)
(8.17) z-7=0 угол 60 о.
z-7=0 угол 60 о. .
.




