Плоскость в пространстве. Получим сначала уравнение плоскости, проходящей через точку М0(х0 ,у0 ,z0 ) перпендикулярно вектору n = {A,B,C },называемому нормалью к плоскости
Получим сначала уравнение плоскости, проходящей через точку М0(х0 ,у0 ,z0) перпендикулярно вектору n = { A,B,C },называемому нормалью к плоскости. Для любой точки плоскости М(х, у, z) вектор М0М = { x - x0 , y - y0, z - z0) ортогонален вектору n, следовательно, их скалярное произведение равно нулю: A(x - x0) + B(y - y0) + C(z - z0) = 0. (8.1) Получено уравнение, которому удовлетворяет любая точка заданной плоскости – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору. После приведения подобных можно записать уравнение (8.1) в виде: Ax + By + Cz + D = 0, (8.2) где D = -Ax0 - By0 - Cz0. Это линейное уравнение относительно трех переменных называют общим уравнением плоскости.
12) A = C = D = 0 – получаем Ву = 0 – уравнение координатной плоскости Охz. 13) B = C = D = 0 – плоскость Ах = 0 является координатной плоскостью Оуz. Если же общее уравнение плоскости является полным (то есть ни один из коэффициентов не равен нулю), его можно привести к виду: называемому уравнением плоскости в отрезках. Способ преобразования показан в лекции 7. Параметры а, b и с равны величинам отрезков, отсекаемых плоскостью на координатных осях.
|

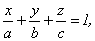 (8.3)
(8.3)


