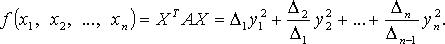Понятие квадратичной формы. Приведение квадратичной формы к каноническому виду.
Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора. Пусть Функция
где Для приведения квадратичной формы к каноническому виду обычно используется метод Лагранжа. Квадратичная форма называется канонической, если все
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы. 1. Ортогональное преобразование пространства
где 2.
Затем подобную процедуру проделывают с квадратичной формой 3. Метод Якоби (в случае, когда все главные миноры
|

 есть векторное пространство над полем
есть векторное пространство над полем 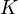 и
и  — базис в
— базис в 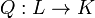 называется квадратичной формой, если её можно представить в виде
называется квадратичной формой, если её можно представить в виде
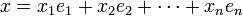 , а
, а  — некоторые элементы поля
— некоторые элементы поля 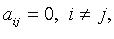 т. е.
т. е.
 :
:
 - собственные значения матрицы A.
- собственные значения матрицы A.
 и т. д. Если в квадратичной форме все
и т. д. Если в квадратичной форме все  но есть
но есть 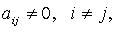 то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например,
то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например,  то полагаем
то полагаем 
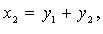

 квадратичной формы отличны от нуля):
квадратичной формы отличны от нуля):