Основна́я теоре́ма а́лгебры утверждает, что
Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.
Самое простое доказательство этой теоремы даётся методами комплексного анализа. Используется тот факт, что функция, аналитическая на всей комплексной плоскости и не имеющая особенностей на бесконечности, есть константа. Посему, функция 1/p, где p — многочлен, должна иметь хоть один полюс на комплексной плоскости, а, соответственно, многочлен имеет хоть один корен
Немедленным следствием из теоремы является то, что любой многочлен степени 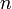 над полем комплексных чисел имеет в нём ровно
над полем комплексных чисел имеет в нём ровно 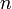 корней, с учётом кратности корней.
корней, с учётом кратности корней.

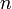 над полем комплексных чисел имеет в нём ровно
над полем комплексных чисел имеет в нём ровно 


