Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
Модуль комплексного числа  обозначается
обозначается 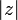 и определяется выражением
и определяется выражением  . Часто обозначается буквами
. Часто обозначается буквами  или
или 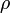 . Если
. Если  является вещественным числом, то
является вещественным числом, то 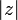 совпадает с абсолютной величиной этого вещественного числа.
совпадает с абсолютной величиной этого вещественного числа.
Для любых  имеют место следующие свойства модуля.:
имеют место следующие свойства модуля.:
1)  , причём
, причём 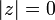 тогда и только тогда, когда
тогда и только тогда, когда  ;;
;;
2)  (неравенство треугольника);
(неравенство треугольника);
3)  ;
;
4) 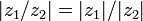 .
.
Из третьего свойства следует 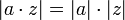 , где
, где 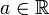 . Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем
. Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем  .
.
5) Для пары комплексных чисел 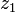 и
и 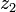 модуль их разности
модуль их разности  равен расстоянию между соответствующими точками комплексной плоскости.
равен расстоянию между соответствующими точками комплексной плоскости.
Угол 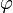 (в радианах) радиус-вектора точки, соответствующей числу
(в радианах) радиус-вектора точки, соответствующей числу  , называется аргументом числа
, называется аргументом числа  и обозначается
и обозначается  .
.
· Из этого определения следует, что  ;
; 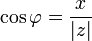 ;
;  .
.
· Для комплексного нуля значение аргумента не определено, для ненулевого числа  аргумент определяется с точностью до
аргумент определяется с точностью до  , где
, где 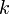 — любое целое число.
— любое целое число.
· Главным значением аргумента называется такое значение 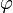 , что
, что 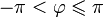 . Часто главное значение обозначается
. Часто главное значение обозначается  [4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного:
[4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного:  .
.

 обозначается
обозначается 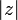 и определяется выражением
и определяется выражением  . Часто обозначается буквами
. Часто обозначается буквами  или
или 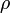 . Если
. Если  имеют место следующие свойства модуля.:
имеют место следующие свойства модуля.: , причём
, причём 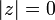 тогда и только тогда, когда
тогда и только тогда, когда  ;;
;; (неравенство треугольника);
(неравенство треугольника); ;
;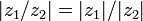 .
.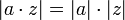 , где
, где 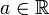 . Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем
. Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем  .
.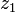 и
и 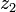 модуль их разности
модуль их разности  равен расстоянию между соответствующими точками комплексной плоскости.
равен расстоянию между соответствующими точками комплексной плоскости.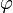 (в радианах) радиус-вектора точки, соответствующей числу
(в радианах) радиус-вектора точки, соответствующей числу  .
. ;
; 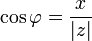 ;
;  .
. , где
, где 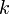 — любое целое число.
— любое целое число.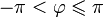 . Часто главное значение обозначается
. Часто главное значение обозначается  [4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного:
[4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного:  .
.


