Алгебраическая форма записи комплексного числа. Арифметические операции с комплексными числами в алгебраической форме записи.
Ко́мпле́ксные чи́сла — расширение множества вещественных чисел, обычно обозначается Запись комплексного числа Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что
Свойство сложени: Сумма двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1+z2= Свойство вычитания: Разность двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1−z2= Свойство умножения: Произведение двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1 Свойство деления: Частное двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z2z1=c+dia+bi=c2+d2ac+bd+c2+d2bc−adi
|

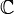 . Любое комплексное число может быть представлено как формальная сумма
. Любое комплексное число может быть представлено как формальная сумма 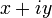 , где
, где 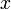 и
и  — вещественные числа,
— вещественные числа, 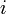 — мнимая единица.
— мнимая единица. в виде
в виде 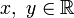 , называется алгебраической формой комплексного числа.
, называется алгебраической формой комплексного числа. ):
):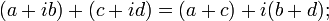
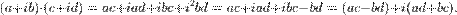
 a+bi
a+bi  +
+  z2=
z2= 


