Вещественное линейное пространство, в котором задано скалярное произведение называется евклидовым пространством.
В трехмерном пространстве модуль вектора равен корню квадратному из скалярного произведения вектора на себя 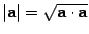 . В евклидовом пространстве модуль вектора определим аналогично
. В евклидовом пространстве модуль вектора определим аналогично
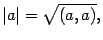
то есть
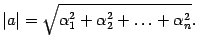
В трехмерном пространстве с помощью склярного произведения определялся угол между векторами. В евклидовом пространстве тоже можно определить угол между векторами. Но угол в  -мерном пространстве не имеет существенного значения, кроме одного случая. В трехмерном проcтранстве два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.
-мерном пространстве не имеет существенного значения, кроме одного случая. В трехмерном проcтранстве два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.
Простейшие свойства линейных пространств. Следующие свойства линейных пространств являются элементарными следствиями из аксиом.
- В линейном пространстве существует единственный нулевой вектор, так как если θ1 и θ2 − два нулевых вектора, то из аксиомы 3 следует, что θ1 = θ1 + θ2 = θ2.
- Для любого вектора линейного пространства существует единственный противоположный вектор, так как если b и c − два противоположных вектора к вектору а, то, последовательно применяя аксиомы 3, 4, 2, получим, что
b = b + (a + c) = (b + a) + c = c. - В линейном пространстве спраедливы равенства: 0а = θ, ∀ a ∈ V и αθ = θ,
∀ α ∈ V.
Доказательство. Для доказательства первого равенства достаточно проверить, что b + 0a = b, ∀ b ∈ V. Это соотношение вытекает из следующей цепочки равенств, основанных на аксиомах 2 - 7: b + 0a = (b + θ) + 0a = b + ((−a) + a) + 0a = (b + (−a)) + a + 0a = (b + (−a)) + 1a + 0a = (b + (−a)) + (1 + 0)a = (b + (-a)) + a =
b + ((-a) + a) = b + θ = b.
Второе равенство доказывается с помощью первого и акстомы 6: если а − произвольный вектор пространства, то αθ = α(0a) = (α0)a = 0a = θ. Доказано. - В линейном пространстве из равенства αa = θ следует, что либо α = 0,
либо а = θ;.
В самом деле, как следует из свойства 3, случай α = 0 возможен, если αa = θ. В случае когда α ≠ 0, на основании свойства 3 и аксиом 5, 6 получим
а = 1а = ((1/α)α)a = (1/α)(αa) = (1/α)θ = θ.
- В линейном пространстве для любого вектоа а противоположный вектор может быть получен как произведение
−a = (−1)a.
Это утверждение вытекает из аксиом 3-5, 7 и свойства 3, так как
a + (−1)a = 1a + (−1)a = (1 - 1)a = 0a = θ.
- Для любой пары векторов a и b линейного пространства существует, и притом единственная, разность b − a.
Доказательство. Вектор b + (-a) являются разностью b − a векторов а и b, так как на основании аксиом 1 - 4 и определения разности имеем
a + (b + (−a) = a + (−a) + b = θ + b = b.
При этом если с − любая другая разность b − a, то из аксиом 2 - 4 следует, что
с = с + θ = c + (a + (−a)) = (c + a) + (−a) = b + (−a). Доказано.

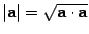 . В евклидовом пространстве модуль вектора определим аналогично
. В евклидовом пространстве модуль вектора определим аналогично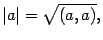
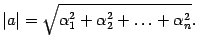
 -мерном пространстве не имеет существенного значения, кроме одного случая. В трехмерном проcтранстве два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.
-мерном пространстве не имеет существенного значения, кроме одного случая. В трехмерном проcтранстве два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.


