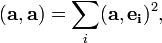Ортонормированный базис конечномерного евклидового пространства.
Ортогональный базис — базис, составленный из попарно ортогональных векторов.
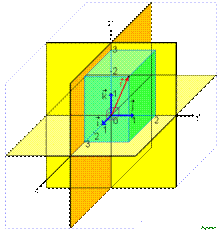
Ортонормированный базис в 3-мерном евклидовом пространстве Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами. Последнее удобно записывается при помощи символа Кронекера:
то есть скалярное произведение каждой пары базисных векторов равно нулю, когда они не совпадают ( Очень многое записывается в ортогональном базисе гораздо проще, чем в произвольном, поэтому очень часто стараются использовать именно такие базисы, если только это возможно или использование какого-то специального неортогонального базиса не дает особых специальных удобств. Или если не отказываются от него в пользу базиса общего вида из соображений общности. Ортонормированный базис является самодуальным (дуальный ему базис совпадает с ним самим). Поэтому в нём можно не делать различия между верхними и нижними индексами, и пользоваться, скажем, только нижними (как обычно и принято, если конечно при этом используются только ортонормированные базисы). Линейная независимость следует из ортогональности, то есть достигается для ортогональной системы векторов автоматически. Коэффициенты в разложении вектора по ортогональному базису:
можно найти так:
Полнота ортонормированной системы векторов эквивалентна равенству Парсеваля: для любого вектора
|
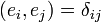
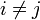), и равно единице при совпадающем индексе, то есть когда берется скалярное произведение любого базисного вектора с самим собой.
.
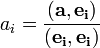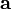квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису:
