Разложение вектора по базису
Определение. Линейной комбинацией векторов  с коэффициентами
с коэффициентами 
 называется вектор
называется вектор 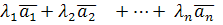 .
.
Говорят, что вектор  раскладывается по векторам
раскладывается по векторам  , если
, если  является линейной комбинацией этих векторов.
является линейной комбинацией этих векторов.
Определение. Векторы  называются линейно зависимыми, если существует такая линейная комбинация
называются линейно зависимыми, если существует такая линейная комбинация 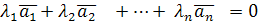 , при не равных нулю одновременно
, при не равных нулю одновременно  i, т.е.
i, т.е.  если же только при
если же только при 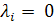 выполняется
выполняется 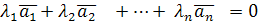 , то векторы называются линейно независимыми.
, то векторы называются линейно независимыми.
Примеры линейных комбинаций векторов:
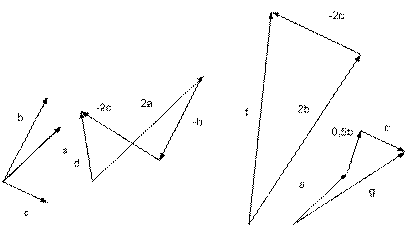
Векторы 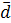 ,
, 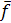 ,
,  на рисунке и
на рисунке и 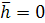 являются линейными комбинациями векторов
являются линейными комбинациями векторов  ,
,  ,
,  :
: 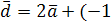 )
) 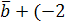 )
)  ,
,  ,
,  ,
, 
Свойства линейно зависимых векторов:
1. Если среди векторов 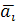 есть нулевой вектор, то эти векторы линейно зависимы.
есть нулевой вектор, то эти векторы линейно зависимы.
2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
4. Любые два коллинеарных вектора линейно зависимы и, наоборот, любые два линейно зависимые векторы коллинеарные.
5. Любые три компланарных вектора линейно зависимы и, наоборот, любые три линейно зависимые вектора компланарны.
6. Любые четыре вектора линейно зависимы.
Справедливы следующие утверждения:
Определение. Система векторов называется базисом пространства 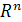 , если векторы этой системы линейно независимы и всякий вектор из
, если векторы этой системы линейно независимы и всякий вектор из 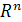 линейно выражается через векторы данной системы.
линейно выражается через векторы данной системы.
Теорема. Разложение любого вектора в базисе, если оно существует, является единственным.
Теорема. Один вектор  линейно зависим тогда и только тогда, когда он нулевой.
линейно зависим тогда и только тогда, когда он нулевой.
Определение. Базисом на прямой  называется любой ненулевой вектор, принадлежащий этой прямой.
называется любой ненулевой вектор, принадлежащий этой прямой.
Теорема. Два вектора 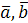 линейно зависимы тогда и только тогда, когда они коллинеарны.
линейно зависимы тогда и только тогда, когда они коллинеарны.
Базисом на плоскости 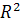 называется любая упорядоченная пара линейно независимых векторов, принадлежащих этой плоскости.
называется любая упорядоченная пара линейно независимых векторов, принадлежащих этой плоскости.
Теорема. Три вектора  линейно зависимы тогда и только тогда, когда они компланарны.
линейно зависимы тогда и только тогда, когда они компланарны.
Определение. Три вектора  являются линейно независимыми, если они не лежат в одной плоскости.
являются линейно независимыми, если они не лежат в одной плоскости.
Базисом в трехмерном пространстве  называется упорядоченная тройка любых линейно независимых векторов.
называется упорядоченная тройка любых линейно независимых векторов.
Если 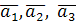 – базис в
– базис в  , то любой другой вектор, например
, то любой другой вектор, например  , единственным образом разлагается по этому базису
, единственным образом разлагается по этому базису
 ,
,
где числа 
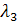 находятся единственным образом и называются координатами вектора
находятся единственным образом и называются координатами вектора  в базисе
в базисе 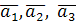 .
.
Определение. Базис 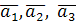 называется ортогональным (прямоугольным), если векторы
называется ортогональным (прямоугольным), если векторы 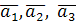 попарно перпендикулярны.
попарно перпендикулярны.
Определение. Ортогональный базис называется ортонормированным, если образующие его векторы имеют длину, равную единице.
Базис в пространстве обычно обозначают 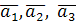 , а ортонормированный базис обозначают
, а ортонормированный базис обозначают  .
.
Пример. Даны векторы 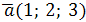 ,
,  ,
, 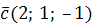 и
и  в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы 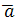 ,
,  и
и  образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 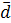 в этом базисе.
в этом базисе.
Решение. Если 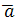 ,
,  и
и  – какие угодно некомпланарные векторы, то всякий вектор
– какие угодно некомпланарные векторы, то всякий вектор 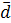 может быть представлен в виде
может быть представлен в виде  , где
, где  – числа.
– числа.
Такое представление вектора и называется разложением его по базису 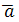 ,
,  ,
,  , а числа
, а числа  – коэффициенты этого разложения являются координатами вектора
– коэффициенты этого разложения являются координатами вектора 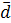 в базисе
в базисе 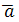 ,
,  ,
,  .
.
Векторы образуют 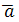 ,
,  и
и  базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:
базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:
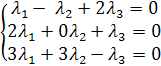 линейно независимы.
линейно независимы.
То есть, если определитель матрицы системы отличен от нуля:
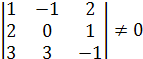 .
.
Вычислим определитель:

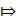 векторы
векторы 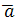 ,
,  и
и  линейно независимые и образуют базис.
линейно независимые и образуют базис.
Запишем разложение вектора 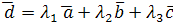 , в координатной форме и решим полученную систему:
, в координатной форме и решим полученную систему:
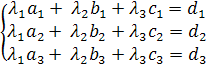 ,
,
для данного примера система имеет вид  . Решаем ее методом Крамера. Уже известен определитель системы
. Решаем ее методом Крамера. Уже известен определитель системы 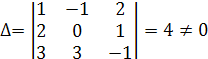 , найдем дополнительные определители и
, найдем дополнительные определители и  :
:
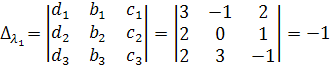 ,
,  ;
;
 ,
,  ;
;
 ,
,  .
.
Ответ: координаты вектора 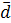 в базисе
в базисе 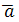 ,
,  ,
,  :
:  .
.
Пример. Найти разложение вектора  в базисе
в базисе 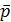 ,
, 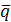 ,
,  , если
, если  ,
,  ,
, 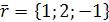 .
.
Решение. Вектор 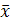 может быть представлен в виде
может быть представлен в виде  (вместо
(вместо 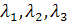 можно обозначить числа
можно обозначить числа 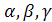 ).
).
Запишем систему и найдем 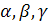 :
:

Ответ: разложение вектора 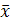 в базисе
в базисе 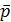 ,
, 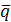 ,
,  имеет вид
имеет вид


 с коэффициентами
с коэффициентами 
 называется вектор
называется вектор 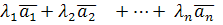 .
. раскладывается по векторам
раскладывается по векторам  , если
, если  называются линейно зависимыми, если существует такая линейная комбинация
называются линейно зависимыми, если существует такая линейная комбинация 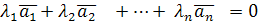 , при не равных нулю одновременно
, при не равных нулю одновременно  i, т.е.
i, т.е.  если же только при
если же только при 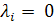 выполняется
выполняется 
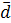 ,
, 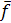 ,
,  на рисунке и
на рисунке и 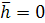 являются линейными комбинациями векторов
являются линейными комбинациями векторов  ,
,  ,
,  :
: 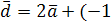 )
) 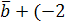 )
)  ,
,  ,
,  ,
, 
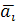 есть нулевой вектор, то эти векторы линейно зависимы.
есть нулевой вектор, то эти векторы линейно зависимы. , если векторы этой системы линейно независимы и всякий вектор из
, если векторы этой системы линейно независимы и всякий вектор из  линейно зависим тогда и только тогда, когда он нулевой.
линейно зависим тогда и только тогда, когда он нулевой. называется любой ненулевой вектор, принадлежащий этой прямой.
называется любой ненулевой вектор, принадлежащий этой прямой. линейно зависимы тогда и только тогда, когда они коллинеарны.
линейно зависимы тогда и только тогда, когда они коллинеарны. называется любая упорядоченная пара линейно независимых векторов, принадлежащих этой плоскости.
называется любая упорядоченная пара линейно независимых векторов, принадлежащих этой плоскости. линейно зависимы тогда и только тогда, когда они компланарны.
линейно зависимы тогда и только тогда, когда они компланарны. являются линейно независимыми, если они не лежат в одной плоскости.
являются линейно независимыми, если они не лежат в одной плоскости. называется упорядоченная тройка любых линейно независимых векторов.
называется упорядоченная тройка любых линейно независимых векторов. – базис в
– базис в  ,
,
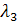 находятся единственным образом и называются координатами вектора
находятся единственным образом и называются координатами вектора  .
.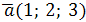 ,
,  ,
, 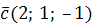 и
и  в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы 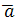 ,
,  образуют базис и найти координаты вектора
образуют базис и найти координаты вектора  , где
, где  – числа.
– числа.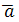 ,
, 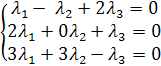 линейно независимы.
линейно независимы.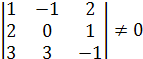 .
.
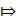 векторы
векторы 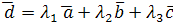 , в координатной форме и решим полученную систему:
, в координатной форме и решим полученную систему: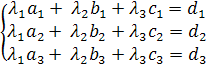 ,
, . Решаем ее методом Крамера. Уже известен определитель системы
. Решаем ее методом Крамера. Уже известен определитель системы 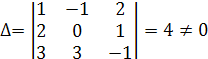 , найдем дополнительные определители и
, найдем дополнительные определители и 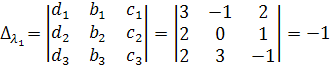 ,
,  ;
; ,
,  ;
; ,
,  .
. .
. в базисе
в базисе 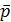 ,
, 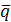 ,
,  , если
, если  ,
,  ,
, 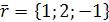 .
.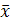 может быть представлен в виде
может быть представлен в виде  (вместо
(вместо 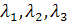 можно обозначить числа
можно обозначить числа 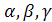 ).
).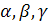 :
:




