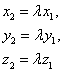Условие коллинеарности и ортогональности векторов
В рассмотрении геометрических векторов вводится определение следующей операции. Произведением вектора Из определения следует, что векторы
Следовательно, равенство (8) выражает условие коллинеарности двух векторов. В рассмотрении векторов, заданных в координатной форме, условие коллинеарности двух векторов (8) примет вид
или
Это векторное равенство справедливо лишь в том случае, если выполняются следующие три скалярных равенства:
или
т.е. необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат. Два вектора называют ортогональными, если их скалярное произведение равно нулю.
|
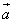на число 
называется вектор, получающийся из вектора 
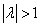) или сжатием (при 
) в 
раз, причём направление вектора 
, и меняется на противоположное, если 
.
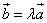всегда расположены на одной или параллельных прямых. Такие векторы называются коллинеарными. Справедливо и обратное утверждение: если векторы 
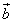коллинеарны, то они связаны соотношением
(8)
