Скалярное произведение и его свойства.
Скаля́рное произведе́ние (в зарубежной литературе - scalar product, dot product, inner product) — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю. · теорема косинусов легко выводится с использованием скалярного произведения:
· Угол между векторами:
· Оценка угла между векторами: в формуле · Проекция вектора
· условие ортогональности[2] (перпендикулярности) векторов
· Площадь параллелограмма, натянутого на два вектора
4. Угол между векторами — угол между направлениями этих векторов (наименьший угол).
По определению, угол между двумя векторами находится в промежутке [0°; 180°].
|


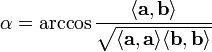
 знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.
знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой. на направление, определяемое единичным вектором
на направление, определяемое единичным вектором 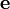 :
: ,
,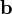 :
:
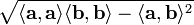

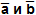 обозначается так:
обозначается так:  .
.


