Свойства. · Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.
· Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения. · Модуль векторного произведения · Если
· Если
· При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны. [править]Алгебраические свойства векторного произведения
8. Смешанное произведение векторов и его свойства 9. Евклидово пространство. Неравенство Коши-Буняковского
|

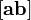 равняется площади
равняется площади 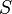 параллелограмма, построенного на приведённых к общему началу векторах
параллелограмма, построенного на приведённых к общему началу векторах  и
и 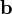 (см. Рисунок 1)
(см. Рисунок 1)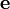 — единичный вектор, ортогональный векторам
— единичный вектор, ортогональный векторам 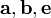 — правая, а
— правая, а 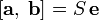
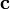 — какой-нибудь вектор,
— какой-нибудь вектор, 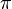 — любая плоскость, содержащая этот вектор,
— любая плоскость, содержащая этот вектор,  — единичный вектор, ортогональный к плоскости
— единичный вектор, ортогональный к плоскости  является правой, то для любого лежащего в плоскости
является правой, то для любого лежащего в плоскости 
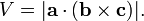
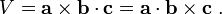
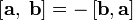
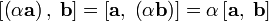
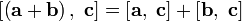
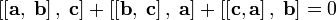
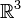 и нарушается в
и нарушается в 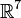
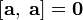
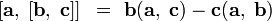
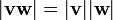 нормы кватернионов
нормы кватернионов
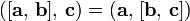
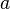 ,
, 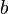 ,
,  и обозначают
и обозначают 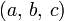 либо
либо 





