ОПТИКА КРИСТАЛЛОВ
2.1. Описание анизотропной среды В этом разделе будут рассмотрены особенности прохождения света через среду, обладающую электрической анизотропией. В естественных условиях к таким средам относятся прежде всего кристаллы. Для подобных сред материальные уравнения, связывающие векторы
Девять величин
Плотность электрической энергии в среде выражается формулой
Изменяя обозначения индексов суммирования (
вычитая почленно (2.3) из (2.4), получим
Поскольку проекции
Такую систему координат в кристалле называют системой главных диэлектрических осей, а соответствующие значения
Выражения (2.5) показывают, что 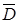 и и  в общем случае имеют различные направления (рис. 8), если только в общем случае имеют различные направления (рис. 8), если только  не совпадает с одной из главных осей или все главные диэлектрические проницаемости не равны друг другу (в последнем случае среда является изотропной). не совпадает с одной из главных осей или все главные диэлектрические проницаемости не равны друг другу (в последнем случае среда является изотропной).
|

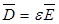 ):
): (2.1)
(2.1) ;
;  образуют тензор диэлектрической проницаемости анизотропной среды. В более компактной форме выражения (2.1) можно записать так:
образуют тензор диэлектрической проницаемости анизотропной среды. В более компактной форме выражения (2.1) можно записать так: ,
,  (2.2)
(2.2) . (2.3)
. (2.3) ), запишем выражение (2.3) в виде
), запишем выражение (2.3) в виде ; (2.4)
; (2.4) .
. ,
,  независимы и в общем случае не равны нулю, из последнего выражения заключаем, что
независимы и в общем случае не равны нулю, из последнего выражения заключаем, что 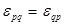 , т.е. тензор диэлектрической проницаемости симметричен. Как известно из курса математики, такой тензор поворотом системы координат может быть приведен к диагональному виду, тогда в этой системе координат связь между векторами
, т.е. тензор диэлектрической проницаемости симметричен. Как известно из курса математики, такой тензор поворотом системы координат может быть приведен к диагональному виду, тогда в этой системе координат связь между векторами  . (2.5)
. (2.5)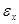 ,
, 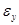 и
и 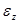 - главными диэлектрическими проницаемостями кристалла. В этой системе объемная плотность электрической энергии может быть выражена двумя различными и наиболее простыми формулами:
- главными диэлектрическими проницаемостями кристалла. В этой системе объемная плотность электрической энергии может быть выражена двумя различными и наиболее простыми формулами: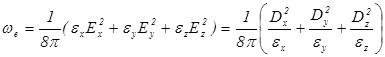 . (2.6)
. (2.6)