В настоящем разделе будут получены соотношения, определяющие условия распространения плоских гармонических световых волн в анизотропной среде. Из первых двух уравнений Максвелла (2.8) для таких волн, исключая 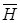 , получим
, получим
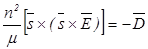 .
.
Отсюда, применяя известное тождество
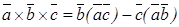 ,
,
получим
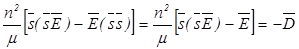 , (2.12)
, (2.12)
что равносильно трем скалярным уравнениям в проекции на главные диэлектрические оси вида
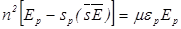 ,
, 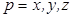 (2.13)
(2.13)
Рассмотрим вначале частные случаи. Пусть вектор  совпадает по направлению с одной из координатных осей, например
совпадает по направлению с одной из координатных осей, например 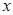 , т.е.
, т.е. 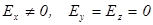 . Следовательно,
. Следовательно, 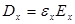 ,
, 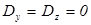 . Тогда в системе уравнений (2.13) останется одно нетривиальное уравнение
. Тогда в системе уравнений (2.13) останется одно нетривиальное уравнение
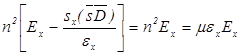 ,
,
откуда
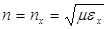
Следовательно, скорость распространения волны, поляризованной вдоль оси 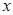 ,
,
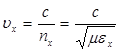 . (2.14)
. (2.14)
Аналогично для скоростей распространения волн, поляризованных вдоль осей 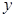 и
и 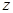 , получим соответственно
, получим соответственно
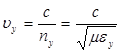 ,
, 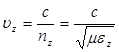 . (2.15)
. (2.15)
Во всех рассмотренных случаях векторы  и
и 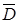 коллинеарны, направления распространения волнового фронта
коллинеарны, направления распространения волнового фронта 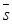 и потока электромагнитной энергии
и потока электромагнитной энергии 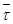 совпадают (
совпадают (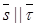 ), причем вектор
), причем вектор 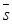 находится в координатной плоскости, ортогональной оси поляризации волны.
находится в координатной плоскости, ортогональной оси поляризации волны.
Скорости 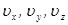 , называют главными скоростями распространения волны в кристалле. Важно отметить, что они не являются проекциями какой-либо иной скорости.
, называют главными скоростями распространения волны в кристалле. Важно отметить, что они не являются проекциями какой-либо иной скорости.
Перейдем к рассмотрению общего случая. Разрешим уравнения (2.13) относительно  :
:
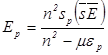 ,
, 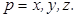 (2.16)
(2.16)
Умножим обе части уравнений (2.16) на 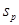 и сложим для всех значений
и сложим для всех значений 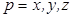 ; в результате получим
; в результате получим
 ,
,
или, после сокращения на (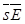 ),
),
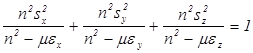 .
.
Представим единицу в правой части в виде 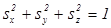 и, перенося ее в левую часть, будем иметь
и, перенося ее в левую часть, будем иметь
 .
.
Учитывая, что 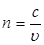 , и соотношения для главных скоростей
, и соотношения для главных скоростей 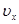 ,
, 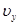 ,
, 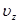 получим окончательно
получим окончательно
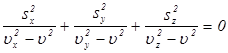 . (2.17)
. (2.17)
Это уравнение называется волновым уравнением Френеля, оно позволяет определить скорость распространения 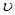 волны в заданном направлении
волны в заданном направлении 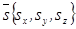 .
.
Рассмотрим решение этого уравнения графическим способом. Из вида уравнения следует, что для каждого его решения 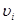 существует решение
существует решение  . Мы будем считать два эти решения одним, так как отрицательные значения скорости соответствуют, очевидно, противоположному направлению движения. Покажем, что уравнение (2.17) имеет два действительных положительных решения. Для этого построим график функции
. Мы будем считать два эти решения одним, так как отрицательные значения скорости соответствуют, очевидно, противоположному направлению движения. Покажем, что уравнение (2.17) имеет два действительных положительных решения. Для этого построим график функции 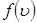 , являющейся левой частью уравнения (2.17).
, являющейся левой частью уравнения (2.17).
В области
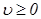
, при условии
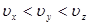
(рис. 10), из графика получаем два корня уравнения (2.17):
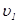
и

.
Таким образом, первый вывод, который следует сделать из нашего рассмотрения, следующий: в анизотропной среде в произвольном направлении 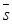 могут распространяться две гармонические волны с фазовыми скоростями
могут распространяться две гармонические волны с фазовыми скоростями 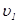 и
и  . Прежде всего отметим, что обе эти волны линейно поляризованы. Действительно, заменив в (2.16)
. Прежде всего отметим, что обе эти волны линейно поляризованы. Действительно, заменив в (2.16) 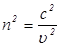 ,
, 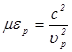 , получим для составляющих вектора
, получим для составляющих вектора 
 ,
, 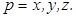 (2.18)
(2.18)
Подставив в (2.I8) 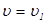 , получим
, получим  , а при
, а при 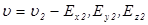 . Легко видеть, что отношения
. Легко видеть, что отношения 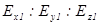 и
и 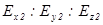 вещественны. А поскольку
вещественны. А поскольку 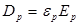 , вещественными будут и соответствующие отношения для векторов
, вещественными будут и соответствующие отношения для векторов 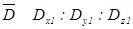 и
и 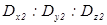 . Из предыдущего раздела известно, что вещественность отношений компонент векторов
. Из предыдущего раздела известно, что вещественность отношений компонент векторов  и
и 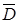 означает, что волны
означает, что волны 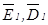 и
и 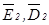 линейно поляризованы. Докажем теперь, что векторы
линейно поляризованы. Докажем теперь, что векторы  и
и  этих волн взаимно ортогональны, для этого применим соотношение (2.12) к обеим волнам, заменив
этих волн взаимно ортогональны, для этого применим соотношение (2.12) к обеим волнам, заменив 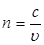 ,
,
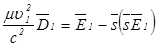 ,
,
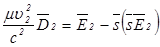 ,
,
умножив скалярно первое уравнение на  , а второе на
, а второе на  , после вычитания получим
, после вычитания получим
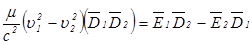 . (2.19)
. (2.19)
Правая часть полученного выражения, как нетрудно убедиться, равна нулю. Следовательно, если 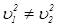 , то
, то 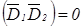 и,следовательно, векторы
и,следовательно, векторы  и
и  , ортогональны.
, ортогональны.
Для дальнейшего изложения необходимо определить так называемый принцип соответствия в кристаллооптике (его доказательство приведено, например, в работах [1, 2]). Сущность этого принципа заключается в следующем: если в любом выражении для кристаллооптики заменить все величины из первого рада (см. ниже) соответствующими величинами из второго ряда, и наоборот, то полученное выражение такие будет иметь правильный физический смысл. Два упомянутых ряда имеют вид
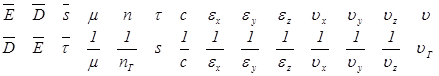
С помощью принципа соответствия можно просто получить ряд полезных соотношений. В частности, из выражения (2.17) посредством указанной замены получим формулу Френеля для лучевой скорости волны, в которой направление луча задано единичным вектором 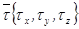 :
:
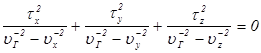 . (2.20)
. (2.20)
Это уравнение такие имеет два решения 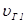 и
и 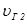 относительно лучевых скоростей. Соответствующие отношения
относительно лучевых скоростей. Соответствующие отношения 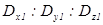 и
и 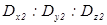 можно найти по выражению, полученному из (2.18):
можно найти по выражению, полученному из (2.18):
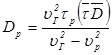 ,
, 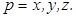
Отсюда аналогично, с помощью материальных уравнений 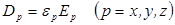 , можно доказать, что отношения
, можно доказать, что отношения 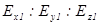 и
и 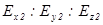 вещественны, т.е. обе эти волны линейно поляризованы. Кроме того, из (2.19) с помощью принципа соответствия также получим, что векторы
вещественны, т.е. обе эти волны линейно поляризованы. Кроме того, из (2.19) с помощью принципа соответствия также получим, что векторы 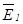 и
и 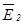 этих волн поляризованы ортогонально друг другу.
этих волн поляризованы ортогонально друг другу.
Таким образом, в общем случае в анизотропной среде вектор 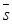 направления распространения волнового фронта и вектор
направления распространения волнового фронта и вектор 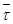 направления распространения энергии не совпадают. Для каждого из этих направлений соответствующие уравнения Френеля определяют фазовые
направления распространения энергии не совпадают. Для каждого из этих направлений соответствующие уравнения Френеля определяют фазовые 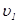 и
и  лучевые
лучевые 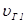 и
и 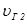 скорости волн, каждая из которых линейно поляризована и направления колебаний векторов
скорости волн, каждая из которых линейно поляризована и направления колебаний векторов  и
и  , в первом случае и векторов
, в первом случае и векторов 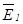 и
и 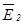 во втором ортогональны друг другу. При этом открытым остается вопрос: каким образом относительно
во втором ортогональны друг другу. При этом открытым остается вопрос: каким образом относительно 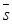 ориентированы векторы
ориентированы векторы  и
и  и относительно
и относительно 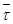 : - векторы
: - векторы 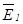 и
и 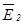 ? Ответ на этот вопрос будет дан в следующем разделе.
? Ответ на этот вопрос будет дан в следующем разделе.
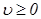 , при условии
, при условии 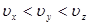 (рис. 10), из графика получаем два корня уравнения (2.17):
(рис. 10), из графика получаем два корня уравнения (2.17): 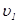 и
и  .
.

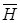 , получим
, получим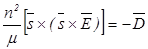 .
.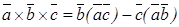 ,
,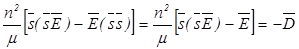 , (2.12)
, (2.12)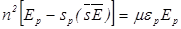 ,
, 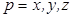 (2.13)
(2.13) совпадает по направлению с одной из координатных осей, например
совпадает по направлению с одной из координатных осей, например 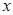 , т.е.
, т.е. 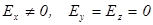 . Следовательно,
. Следовательно, 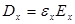 ,
, 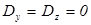 . Тогда в системе уравнений (2.13) останется одно нетривиальное уравнение
. Тогда в системе уравнений (2.13) останется одно нетривиальное уравнение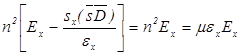 ,
,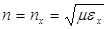
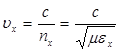 . (2.14)
. (2.14) и
и  , получим соответственно
, получим соответственно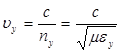 ,
, 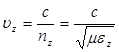 . (2.15)
. (2.15)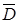 коллинеарны, направления распространения волнового фронта
коллинеарны, направления распространения волнового фронта 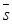 и потока электромагнитной энергии
и потока электромагнитной энергии 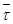 совпадают (
совпадают (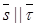 ), причем вектор
), причем вектор 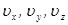 , называют главными скоростями распространения волны в кристалле. Важно отметить, что они не являются проекциями какой-либо иной скорости.
, называют главными скоростями распространения волны в кристалле. Важно отметить, что они не являются проекциями какой-либо иной скорости. :
: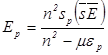 ,
, 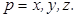 (2.16)
(2.16)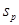 и сложим для всех значений
и сложим для всех значений  ,
,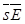 ),
),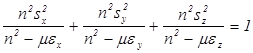 .
.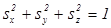 и, перенося ее в левую часть, будем иметь
и, перенося ее в левую часть, будем иметь .
.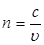 , и соотношения для главных скоростей
, и соотношения для главных скоростей 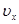 ,
, 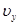 ,
, 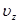 получим окончательно
получим окончательно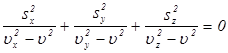 . (2.17)
. (2.17)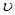 волны в заданном направлении
волны в заданном направлении 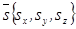 .
.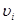 существует решение
существует решение  . Мы будем считать два эти решения одним, так как отрицательные значения скорости соответствуют, очевидно, противоположному направлению движения. Покажем, что уравнение (2.17) имеет два действительных положительных решения. Для этого построим график функции
. Мы будем считать два эти решения одним, так как отрицательные значения скорости соответствуют, очевидно, противоположному направлению движения. Покажем, что уравнение (2.17) имеет два действительных положительных решения. Для этого построим график функции 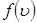 , являющейся левой частью уравнения (2.17).
, являющейся левой частью уравнения (2.17).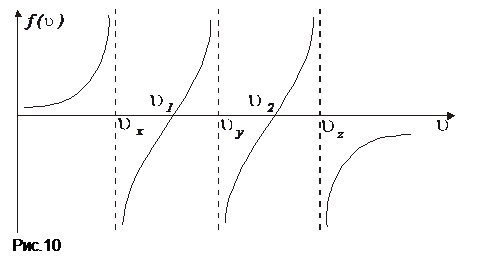
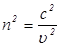 ,
,  , получим для составляющих вектора
, получим для составляющих вектора  ,
, 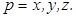 (2.18)
(2.18)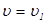 , получим
, получим  , а при
, а при 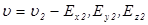 . Легко видеть, что отношения
. Легко видеть, что отношения 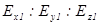 и
и 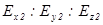 вещественны. А поскольку
вещественны. А поскольку 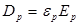 , вещественными будут и соответствующие отношения для векторов
, вещественными будут и соответствующие отношения для векторов 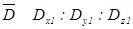 и
и 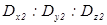 . Из предыдущего раздела известно, что вещественность отношений компонент векторов
. Из предыдущего раздела известно, что вещественность отношений компонент векторов 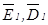 и
и 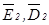 линейно поляризованы. Докажем теперь, что векторы
линейно поляризованы. Докажем теперь, что векторы  и
и  этих волн взаимно ортогональны, для этого применим соотношение (2.12) к обеим волнам, заменив
этих волн взаимно ортогональны, для этого применим соотношение (2.12) к обеим волнам, заменив 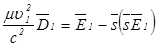 ,
,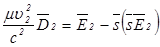 ,
,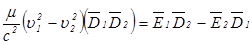 . (2.19)
. (2.19)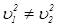 , то
, то 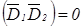 и,следовательно, векторы
и,следовательно, векторы 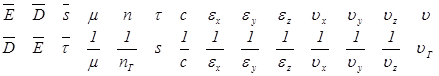
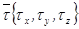 :
: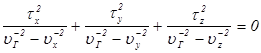 . (2.20)
. (2.20) и
и  относительно лучевых скоростей. Соответствующие отношения
относительно лучевых скоростей. Соответствующие отношения 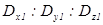 и
и 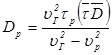 ,
, 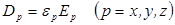 , можно доказать, что отношения
, можно доказать, что отношения 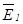 и
и 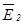 этих волн поляризованы ортогонально друг другу.
этих волн поляризованы ортогонально друг другу.


