Рассмотрим частные случаи вырождения двуосного кристалла в одноосный. Это возможно в двух случаях:
1) 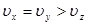 , положительный кристалл
, положительный кристалл  , оптическая ось совпадает с осью
, оптическая ось совпадает с осью 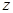 . Уравнение лучевой поверхности распадается на уравнение сферы с радиусом
. Уравнение лучевой поверхности распадается на уравнение сферы с радиусом 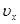 и эллипсоида вокруг оси
и эллипсоида вокруг оси 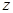 , вписанного в сферу:
, вписанного в сферу:
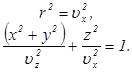
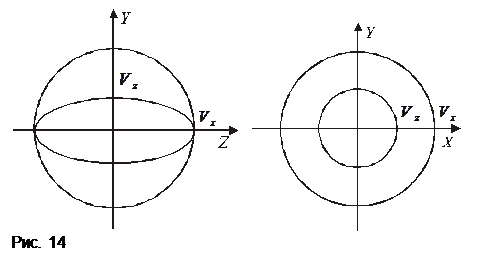
Сечения лучевой поверхности координатными плоскостями показаны на рис. 14;
2) 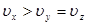 , отрицательный кристалл
, отрицательный кристалл 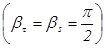 , оптическая ось кристалла совпадает с осью
, оптическая ось кристалла совпадает с осью 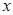 . Уравнение лучевой поверхности распадается на уравнение сферы с радиусом
. Уравнение лучевой поверхности распадается на уравнение сферы с радиусом 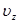 и эллипсоида вращения вокруг оси
и эллипсоида вращения вокруг оси 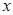 , описанного вокруг сферы:
, описанного вокруг сферы:

Сечения лучевой поверхности координатными плоскостями показаны на рис. 15.
Поскольку одна из полостей лучевой поверхности - сфера, то при изменении положения вектора

: скорость одной из волн остается постоянной; соответствующую волну называют обыкновенной, ее скорость обозначают
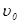
, а показатель преломления -

. Скорость другой волны при изменении

меняется, поэтому такую волну называют необыкновенной, ее скорость обозначают
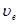
, а показатель преломления

. Для положительного одноосного кристалла
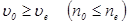
, для отрицательного
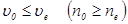
.
Уместно заметить, что задаваемые в справочниках значения  равны максимальным значениям для положительного кристалла и минимальным - для отрицательного. Обратимся к рис. 16, где представлен лучевой эллипсоид Френеля для отрицательного одноосного кристалла. Плоскость, составленная вектором
равны максимальным значениям для положительного кристалла и минимальным - для отрицательного. Обратимся к рис. 16, где представлен лучевой эллипсоид Френеля для отрицательного одноосного кристалла. Плоскость, составленная вектором  луча и оптической осью
луча и оптической осью 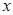 , называется главной плоскостью. Как видно из рисунка, при изменении положения вектора
, называется главной плоскостью. Как видно из рисунка, при изменении положения вектора  обыкновенная волна имеет постоянную скорость
обыкновенная волна имеет постоянную скорость 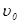 и ее вектор
и ее вектор 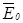 колеблется перпендикулярно главной плоскости. Скорость необыкновенной волны
колеблется перпендикулярно главной плоскости. Скорость необыкновенной волны 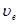 изменяется, а вектор
изменяется, а вектор  колеблется в главной
колеблется в главной
плоскости.
 : скорость одной из волн остается постоянной; соответствующую волну называют обыкновенной, ее скорость обозначают
: скорость одной из волн остается постоянной; соответствующую волну называют обыкновенной, ее скорость обозначают 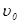 , а показатель преломления -
, а показатель преломления -  . Скорость другой волны при изменении
. Скорость другой волны при изменении  меняется, поэтому такую волну называют необыкновенной, ее скорость обозначают
меняется, поэтому такую волну называют необыкновенной, ее скорость обозначают 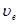 , а показатель преломления
, а показатель преломления  . Для положительного одноосного кристалла
. Для положительного одноосного кристалла 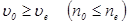 , для отрицательного
, для отрицательного 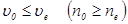 .
.

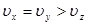 , положительный кристалл
, положительный кристалл  , оптическая ось совпадает с осью
, оптическая ось совпадает с осью 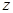 . Уравнение лучевой поверхности распадается на уравнение сферы с радиусом
. Уравнение лучевой поверхности распадается на уравнение сферы с радиусом 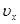 и эллипсоида вокруг оси
и эллипсоида вокруг оси 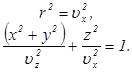
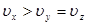 , отрицательный кристалл
, отрицательный кристалл 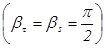 , оптическая ось кристалла совпадает с осью
, оптическая ось кристалла совпадает с осью 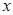 . Уравнение лучевой поверхности распадается на уравнение сферы с радиусом
. Уравнение лучевой поверхности распадается на уравнение сферы с радиусом 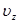 и эллипсоида вращения вокруг оси
и эллипсоида вращения вокруг оси 

 равны максимальным значениям для положительного кристалла и минимальным - для отрицательного. Обратимся к рис. 16, где представлен лучевой эллипсоид Френеля для отрицательного одноосного кристалла. Плоскость, составленная вектором
равны максимальным значениям для положительного кристалла и минимальным - для отрицательного. Обратимся к рис. 16, где представлен лучевой эллипсоид Френеля для отрицательного одноосного кристалла. Плоскость, составленная вектором 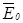 колеблется перпендикулярно главной плоскости. Скорость необыкновенной волны
колеблется перпендикулярно главной плоскости. Скорость необыкновенной волны  колеблется в главной
колеблется в главной 



