Рассмотрим плоскую гармоническую волну с частотой 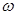 , распространяющуюся в кристалле в направлении
, распространяющуюся в кристалле в направлении 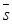 . Тогда векторы
. Тогда векторы  ,
, 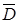 ,
, 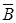 и
и 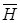 такой волны можно записать в виде
такой волны можно записать в виде
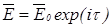 ,
,  ,
, 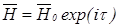 ,
, 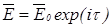 , (2.7)
, (2.7)
где  ,
, 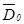 ,
, 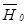 - амплитуды волн;
- амплитуды волн;  - пространственно-временной параметр, характеризующий плоскую волну (фаза волны).
- пространственно-временной параметр, характеризующий плоскую волну (фаза волны).
Подставим выражения (2.7) в уравнения Максвелла (1.1) - (1.4), при этом учтем, что действие операторов  и
и  на векторы поля равносильно умножению на эти векторы величин
на векторы поля равносильно умножению на эти векторы величин 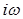 и
и 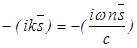 соответственно. Тогда после преобразований получим
соответственно. Тогда после преобразований получим
 (2.8)
(2.8)
где 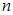 - показатель преломления.
- показатель преломления.
Из уравнения (2.8) видно, что вектор 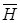 и, следовательно, вектор
и, следовательно, вектор  перпендикулярны векторам
перпендикулярны векторам  ,
, 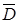 и
и 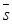 , которые поэтому должны быть компланарны. Кроме того, вектор
, которые поэтому должны быть компланарны. Кроме того, вектор 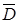 ортогонален
ортогонален 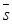 . Следовательно, векторы
. Следовательно, векторы 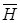 и
и 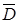 перпендикулярны к направлению распространения волны
перпендикулярны к направлению распространения волны 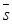 , а вектор
, а вектор  составляет с ним некоторый угол, в общем случае отличный от прямого (рис. 9).
составляет с ним некоторый угол, в общем случае отличный от прямого (рис. 9).
Направление распространения электромагнитной энергии, как известно, характеризуется вектором Пойнтинга:
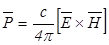
.
Введем единичный вектор 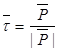 , характеризующий это направление, тогда получим, что векторы
, характеризующий это направление, тогда получим, что векторы 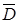 ,
, 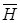 и
и 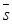 с одной стороны, и
с одной стороны, и  ,
, 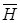 и
и 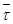 -с другой, образуют ортогональные тройки векторов с общим вектором
-с другой, образуют ортогональные тройки векторов с общим вектором 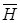 , повернутые относительно друг друга на угол
, повернутые относительно друг друга на угол 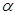 . Таким образом, в анизотропной среде в отличие от изотропной направление распространения энергии (луча)
. Таким образом, в анизотропной среде в отличие от изотропной направление распространения энергии (луча) 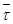 не совпадает с направлением распространения волнового фронта
не совпадает с направлением распространения волнового фронта 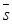 . Вместе с тем равенство плотностей электрической и магнитной энергий сохраняется. Действительно, из (2.8) получим
. Вместе с тем равенство плотностей электрической и магнитной энергий сохраняется. Действительно, из (2.8) получим
 ;
;  ,
,
откуда видно, что, согласно свойствам смешанного произведения векторов, 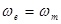 . Полная плотность электромагнитной энергии
. Полная плотность электромагнитной энергии
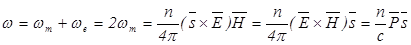 .(2.9)
.(2.9)
Из последнего выражения получим
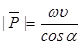 , (2.10)
, (2.10)
где 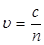 - фазовая скорость волны.
- фазовая скорость волны.
Сравнив (2.10) и (1.13), можно заметить, что величина
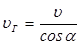 (2.11)
(2.11)
характеризует скорость распространения энергии; поэтому она называется групповой, или лучевой, скоростью. Очевидно, что отношение 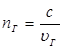 определяет лучевой, или групповой, показатель преломления, который связан с фазовым как
определяет лучевой, или групповой, показатель преломления, который связан с фазовым как
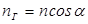 .
.
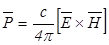 .
.

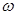 , распространяющуюся в кристалле в направлении
, распространяющуюся в кристалле в направлении 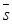 . Тогда векторы
. Тогда векторы  ,
, 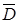 ,
, 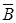 и
и 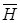 такой волны можно записать в виде
такой волны можно записать в виде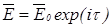 ,
,  ,
, 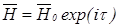 ,
,  ,
, 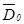 ,
, 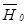 - амплитуды волн;
- амплитуды волн;  - пространственно-временной параметр, характеризующий плоскую волну (фаза волны).
- пространственно-временной параметр, характеризующий плоскую волну (фаза волны). и
и  на векторы поля равносильно умножению на эти векторы величин
на векторы поля равносильно умножению на эти векторы величин 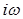 и
и 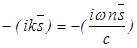 соответственно. Тогда после преобразований получим
соответственно. Тогда после преобразований получим (2.8)
(2.8)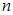 - показатель преломления.
- показатель преломления. перпендикулярны векторам
перпендикулярны векторам 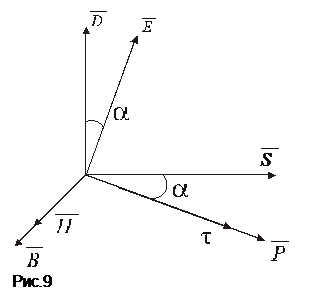
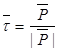 , характеризующий это направление, тогда получим, что векторы
, характеризующий это направление, тогда получим, что векторы 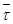 -с другой, образуют ортогональные тройки векторов с общим вектором
-с другой, образуют ортогональные тройки векторов с общим вектором 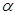 . Таким образом, в анизотропной среде в отличие от изотропной направление распространения энергии (луча)
. Таким образом, в анизотропной среде в отличие от изотропной направление распространения энергии (луча)  ;
;  ,
,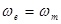 . Полная плотность электромагнитной энергии
. Полная плотность электромагнитной энергии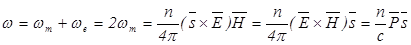 .(2.9)
.(2.9)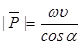 , (2.10)
, (2.10)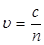 - фазовая скорость волны.
- фазовая скорость волны.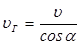 (2.11)
(2.11)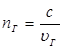 определяет лучевой, или групповой, показатель преломления, который связан с фазовым как
определяет лучевой, или групповой, показатель преломления, который связан с фазовым как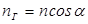 .
.


