Искусственной анизотропией называют явление возникновения анизотропных свойств у оптических изотропных тел под действием механических напряжений, электрических и магнитных полей.
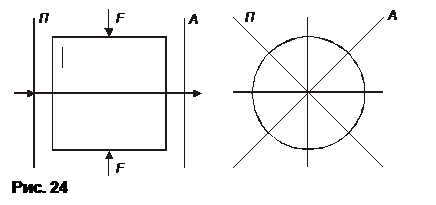 Анизотропия при деформации. Многие изотропные вещества при деформации сжатия или растяжения (рис. 24) приобретают свойства одноосного кристалла, оптическая ось которого направлена вдоль деформирующих сил. При этом разность показателей преломления необыкновенной и обыкновенной волн определяется зависимостью
Анизотропия при деформации. Многие изотропные вещества при деформации сжатия или растяжения (рис. 24) приобретают свойства одноосного кристалла, оптическая ось которого направлена вдоль деформирующих сил. При этом разность показателей преломления необыкновенной и обыкновенной волн определяется зависимостью
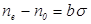 .
.
где  - постоянная, характеризующая свойства вещества;
- постоянная, характеризующая свойства вещества; 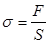 - напряжение деформации, равное отношению силы к площади поперечного сечения образца.
- напряжение деформации, равное отношению силы к площади поперечного сечения образца.
При наблюдении прозрачного деформированного образца в скрещенных поляризаторе и анализаторе он оказывается окрашенным, причем окраска зависит от степени деформации.
Анизотропия под воздействием электрического поля. Оптически изотропные вещества под действием электрического поля (рис. 25) приобретают свойства одноосного кристалла, оптическая ось которого коллинеарна напряженности электрического поля (явление Керра). Анизотропия (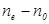 ) при этом определяется соотношением
) при этом определяется соотношением
 ,
,
где  - постоянная Керра, характеризующая вещество;
- постоянная Керра, характеризующая вещество; 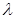 - длина волны света;
- длина волны света;  - напряженность электрического поля.
- напряженность электрического поля.

Для некоторых жидкостей величина  достигает значений
достигает значений 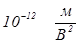 , для газов она значительно меньше. Эффект Керра обладает очень малой инерционностью (оптическая анизотропия следует за изменением напряженности электрического поля с запаздыванием порядка
, для газов она значительно меньше. Эффект Керра обладает очень малой инерционностью (оптическая анизотропия следует за изменением напряженности электрического поля с запаздыванием порядка 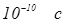 ), поэтому он позволяет создавать быстродействующие модуляторы света, называемые ячейками Керра.
), поэтому он позволяет создавать быстродействующие модуляторы света, называемые ячейками Керра.
Обычно такую ячейку помещают между скрещенными поляризатором и анализатором так что оптическая ось составляет углы по 45 град. с их главными плоскостями. При отсутствии напряжения на электродах ячейка закрыта - свет не выходит из анализатора. При увеличении напряженности поля в ячейке свет начинает проходить через нее, и при определенном значении напряженности  возникающая разность хода на длине
возникающая разность хода на длине 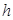 ячейки равна
ячейки равна  , т.е.
, т.е.
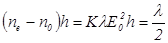
- пропускание ячейки становится максимальным. Соответствующая напряженность 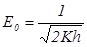 . Напряжение
. Напряжение 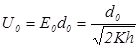 называется полуволновым, для реальных ячеек Керра оно составляет несколько сотен вольт.
называется полуволновым, для реальных ячеек Керра оно составляет несколько сотен вольт.
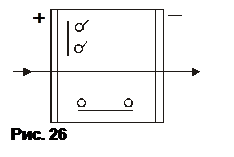 Другим электрооптическим эффектом является эффект Поккельса. Он возникает в некоторых одноосных кристаллах при приложении электрического поля. В зависимости от направления приложенного поля различают продольный и поперечный эффект Поккельса. В первом случае электрическое поле направлено вдоль собственной оптической оси ОО кристалла (рис. 26). Для прохождения света либо делают электроды прозрачными, либо выполняют в них отверстия. При наличии внешнего электрического поля в кристалле возникают вторая оптическая ось О"О', ортогональная собственной оси кристалла, и двойное лучепреломление, определяемое выражением
Другим электрооптическим эффектом является эффект Поккельса. Он возникает в некоторых одноосных кристаллах при приложении электрического поля. В зависимости от направления приложенного поля различают продольный и поперечный эффект Поккельса. В первом случае электрическое поле направлено вдоль собственной оптической оси ОО кристалла (рис. 26). Для прохождения света либо делают электроды прозрачными, либо выполняют в них отверстия. При наличии внешнего электрического поля в кристалле возникают вторая оптическая ось О"О', ортогональная собственной оси кристалла, и двойное лучепреломление, определяемое выражением
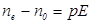 ,
,
где  - постоянная Поккельса. Во втором случае электрическое поле перпендикулярно собственной оси кристалла, а наведенная оптическая ось параллельна внешнему электрическому полю. На основе эффекта Поккельса такие изготовляют быстродействующие модуляторы света - ячейки Поккельса. Несомненным преимуществом этих ячеек является значительно меньшее значение полуволнового напряжения.
- постоянная Поккельса. Во втором случае электрическое поле перпендикулярно собственной оси кристалла, а наведенная оптическая ось параллельна внешнему электрическому полю. На основе эффекта Поккельса такие изготовляют быстродействующие модуляторы света - ячейки Поккельса. Несомненным преимуществом этих ячеек является значительно меньшее значение полуволнового напряжения.
 Анизотропия под действием магнитного поля. Некоторые оптически изотропные вещества в магнитном поле (рис. 27) приобретают свойства одноосного кристалла, ось которого коллинеарна индукции
Анизотропия под действием магнитного поля. Некоторые оптически изотропные вещества в магнитном поле (рис. 27) приобретают свойства одноосного кристалла, ось которого коллинеарна индукции 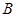 магнитного поля (эффект Коттон - Мутона). При этом
магнитного поля (эффект Коттон - Мутона). При этом
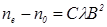 ,
,
где 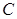 - постоянная Коттон - Мутона, характеризующая свойства вещества. Например, для нитробензола
- постоянная Коттон - Мутона, характеризующая свойства вещества. Например, для нитробензола 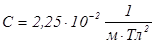 . Другим примером искусственной анизотропии в магнитном поле является эффект Фарадея, заключающийся в том, что некоторые вещества в магнитном поле, напряженность
. Другим примером искусственной анизотропии в магнитном поле является эффект Фарадея, заключающийся в том, что некоторые вещества в магнитном поле, напряженность 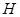 которого коллинеарна световому лучу, приобретают свойства оптической активности. При этом угол поворота плоскости поляризации определяется соотношением
которого коллинеарна световому лучу, приобретают свойства оптической активности. При этом угол поворота плоскости поляризации определяется соотношением
 ,
,
где 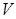 - постоянная Верде, характеризующая свойства вещества;
- постоянная Верде, характеризующая свойства вещества; 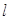 - длина хода луча в веществе.
- длина хода луча в веществе.
Угол поворота 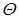 невелик. Для большинства твердых тел при напряженности поля
невелик. Для большинства твердых тел при напряженности поля  и
и 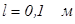 угол поворота составляет 1…2 град.
угол поворота составляет 1…2 град.
2.10. Задачи и примеры
1. Главные диэлектрические проницаемости среды: 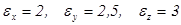 . Магнитная проницаемость
. Магнитная проницаемость 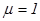 . Найти фазовые скорости плоских гармонических волн, распространявшихся в направлении
. Найти фазовые скорости плоских гармонических волн, распространявшихся в направлении 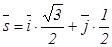 . Как поляризованы эти волны?
. Как поляризованы эти волны?
Решение. Для нахождения фазовых скоростей волн воспользуемся уравнением Френеля (2.17), которое запишем в виде
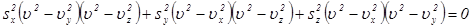 .
.
Полагая здесь 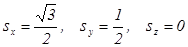 , получим два уравнения:
, получим два уравнения:

решив которые, найдем два неотрицательных значения фазовой скорости волн:
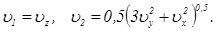
Подставляя в эти выражения значения главных скоростей  , получим
, получим  . Обозначим амплитуду вектора
. Обозначим амплитуду вектора 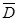 первой волны
первой волны 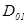 , второй -
, второй - 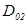 , тогда уравнения волн можно записать в виде
, тогда уравнения волн можно записать в виде
 ,
,
где  - частота волны,
- частота волны, 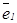 и
и 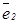 - единичные векторы, ортогональные
- единичные векторы, ортогональные 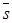 и определяющие поляризацию волн (см. рис. 12). Так как
и определяющие поляризацию волн (см. рис. 12). Так как  то, очевидно,
то, очевидно, 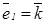 ,т.е. волна
,т.е. волна 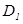 поляризована вдоль оси
поляризована вдоль оси 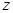 . Вектор
. Вектор 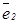 ортогонален оси
ортогонален оси 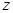 и может быть записан в виде
и может быть записан в виде 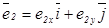 . Так как модуль вектора
. Так как модуль вектора 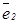 равен единице, а сам вектор ортогонален
равен единице, а сам вектор ортогонален 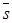 , можно записать два выражения:
, можно записать два выражения:
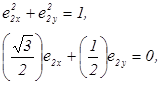
откуда получим 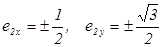 .
.
Предлагаем читателю в виде упражнения сделать графическую иллюстрацию к этой задаче.
2. Плоская пластина толщиной 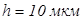 вырезана из одноосного кристалла так, что оптическая ось параллельна плоскости пластины. На пластину нормально падает линейно поляризованная волна
вырезана из одноосного кристалла так, что оптическая ось параллельна плоскости пластины. На пластину нормально падает линейно поляризованная волна 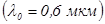 единичной интенсивности, плоскость колебаний которой составляет угол
единичной интенсивности, плоскость колебаний которой составляет угол 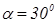 с оптической осью. Как будет поляризована волна на выходе, если показатели преломления для обыкновенной и необыкновенной волн равны соответственно
с оптической осью. Как будет поляризована волна на выходе, если показатели преломления для обыкновенной и необыкновенной волн равны соответственно 
Решение. Указанная пластина является фазовой пластинкой. Найдем вносимую ею разность фаз:
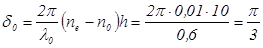 .
.
Введем в плоскости пластины систему координат  , ось
, ось  которой совмещена с оптической осью. Так как
которой совмещена с оптической осью. Так как 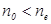 (кристалл положительный), то
(кристалл положительный), то 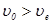 , а поскольку обыкновенная волна поляризована вдоль оси
, а поскольку обыкновенная волна поляризована вдоль оси 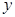 , то ось
, то ось 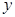 является "быстрой" осью фазовой пластинки. Матрица Джонса этой пластинки (см. табл. 2 для
является "быстрой" осью фазовой пластинки. Матрица Джонса этой пластинки (см. табл. 2 для 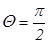 ) имеет вид
) имеет вид
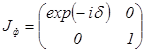 .
.
Вектор Джонса падающей волны запишем в виде
 ,
,
тогда вектор Джонса на выходе
 ,
,
т.е. волна эллиптически поляризована с правым вращением вектора 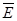 . Параметры эллипса поляризации предлагаем читателю определить самостоятельно (см. разд. 1).
. Параметры эллипса поляризации предлагаем читателю определить самостоятельно (см. разд. 1).
3. На призму Волластона (см. рис. 22г), изготовленную из исландского шпата 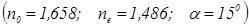 падает нормально к передней грани луч света. Найти угол между выходящими из призмы лучами.
падает нормально к передней грани луч света. Найти угол между выходящими из призмы лучами.
Решение. При переходе через границу раздела между средами с взаимно перпендикулярными оптическими осями обыкновенный в первой среде луч становится необыкновенным во второй, и наоборот. Обозначая через  и
и 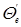 углы преломления обыкновенного и необыкновенного лучей, можно записать (углы падения
углы преломления обыкновенного и необыкновенного лучей, можно записать (углы падения  )
)
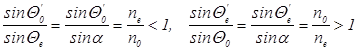 .
.
При выходе из призмы в воздух углы падения для указанных лучей будут равны соответственно  и
и 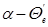 .Углы преломления
.Углы преломления  и
и  этих лучей найдем из закона преломления:
этих лучей найдем из закона преломления:
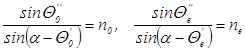 .
.
Решая попарно полученные уравнения, найдем  ;
;  , поэтому угол между выходящими лучами
, поэтому угол между выходящими лучами  .
.

 Анизотропия при деформации. Многие изотропные вещества при деформации сжатия или растяжения (рис. 24) приобретают свойства одноосного кристалла, оптическая ось которого направлена вдоль деформирующих сил. При этом разность показателей преломления необыкновенной и обыкновенной волн определяется зависимостью
Анизотропия при деформации. Многие изотропные вещества при деформации сжатия или растяжения (рис. 24) приобретают свойства одноосного кристалла, оптическая ось которого направлена вдоль деформирующих сил. При этом разность показателей преломления необыкновенной и обыкновенной волн определяется зависимостью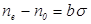 .
. - постоянная, характеризующая свойства вещества;
- постоянная, характеризующая свойства вещества; 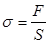 - напряжение деформации, равное отношению силы к площади поперечного сечения образца.
- напряжение деформации, равное отношению силы к площади поперечного сечения образца.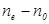 ) при этом определяется соотношением
) при этом определяется соотношением ,
, - постоянная Керра, характеризующая вещество;
- постоянная Керра, характеризующая вещество; 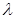 - длина волны света;
- длина волны света;  - напряженность электрического поля.
- напряженность электрического поля.
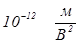 , для газов она значительно меньше. Эффект Керра обладает очень малой инерционностью (оптическая анизотропия следует за изменением напряженности электрического поля с запаздыванием порядка
, для газов она значительно меньше. Эффект Керра обладает очень малой инерционностью (оптическая анизотропия следует за изменением напряженности электрического поля с запаздыванием порядка 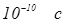 ), поэтому он позволяет создавать быстродействующие модуляторы света, называемые ячейками Керра.
), поэтому он позволяет создавать быстродействующие модуляторы света, называемые ячейками Керра. возникающая разность хода на длине
возникающая разность хода на длине 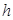 ячейки равна
ячейки равна  , т.е.
, т.е.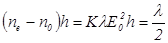
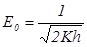 . Напряжение
. Напряжение 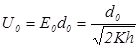 называется полуволновым, для реальных ячеек Керра оно составляет несколько сотен вольт.
называется полуволновым, для реальных ячеек Керра оно составляет несколько сотен вольт. Другим электрооптическим эффектом является эффект Поккельса. Он возникает в некоторых одноосных кристаллах при приложении электрического поля. В зависимости от направления приложенного поля различают продольный и поперечный эффект Поккельса. В первом случае электрическое поле направлено вдоль собственной оптической оси ОО кристалла (рис. 26). Для прохождения света либо делают электроды прозрачными, либо выполняют в них отверстия. При наличии внешнего электрического поля в кристалле возникают вторая оптическая ось О"О', ортогональная собственной оси кристалла, и двойное лучепреломление, определяемое выражением
Другим электрооптическим эффектом является эффект Поккельса. Он возникает в некоторых одноосных кристаллах при приложении электрического поля. В зависимости от направления приложенного поля различают продольный и поперечный эффект Поккельса. В первом случае электрическое поле направлено вдоль собственной оптической оси ОО кристалла (рис. 26). Для прохождения света либо делают электроды прозрачными, либо выполняют в них отверстия. При наличии внешнего электрического поля в кристалле возникают вторая оптическая ось О"О', ортогональная собственной оси кристалла, и двойное лучепреломление, определяемое выражением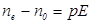 ,
, - постоянная Поккельса. Во втором случае электрическое поле перпендикулярно собственной оси кристалла, а наведенная оптическая ось параллельна внешнему электрическому полю. На основе эффекта Поккельса такие изготовляют быстродействующие модуляторы света - ячейки Поккельса. Несомненным преимуществом этих ячеек является значительно меньшее значение полуволнового напряжения.
- постоянная Поккельса. Во втором случае электрическое поле перпендикулярно собственной оси кристалла, а наведенная оптическая ось параллельна внешнему электрическому полю. На основе эффекта Поккельса такие изготовляют быстродействующие модуляторы света - ячейки Поккельса. Несомненным преимуществом этих ячеек является значительно меньшее значение полуволнового напряжения. Анизотропия под действием магнитного поля. Некоторые оптически изотропные вещества в магнитном поле (рис. 27) приобретают свойства одноосного кристалла, ось которого коллинеарна индукции
Анизотропия под действием магнитного поля. Некоторые оптически изотропные вещества в магнитном поле (рис. 27) приобретают свойства одноосного кристалла, ось которого коллинеарна индукции 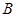 магнитного поля (эффект Коттон - Мутона). При этом
магнитного поля (эффект Коттон - Мутона). При этом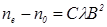 ,
,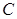 - постоянная Коттон - Мутона, характеризующая свойства вещества. Например, для нитробензола
- постоянная Коттон - Мутона, характеризующая свойства вещества. Например, для нитробензола 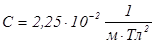 . Другим примером искусственной анизотропии в магнитном поле является эффект Фарадея, заключающийся в том, что некоторые вещества в магнитном поле, напряженность
. Другим примером искусственной анизотропии в магнитном поле является эффект Фарадея, заключающийся в том, что некоторые вещества в магнитном поле, напряженность 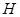 которого коллинеарна световому лучу, приобретают свойства оптической активности. При этом угол поворота плоскости поляризации определяется соотношением
которого коллинеарна световому лучу, приобретают свойства оптической активности. При этом угол поворота плоскости поляризации определяется соотношением ,
,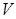 - постоянная Верде, характеризующая свойства вещества;
- постоянная Верде, характеризующая свойства вещества; 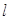 - длина хода луча в веществе.
- длина хода луча в веществе.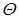 невелик. Для большинства твердых тел при напряженности поля
невелик. Для большинства твердых тел при напряженности поля  и
и 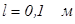 угол поворота составляет 1…2 град.
угол поворота составляет 1…2 град.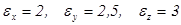 . Магнитная проницаемость
. Магнитная проницаемость 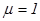 . Найти фазовые скорости плоских гармонических волн, распространявшихся в направлении
. Найти фазовые скорости плоских гармонических волн, распространявшихся в направлении 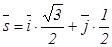 . Как поляризованы эти волны?
. Как поляризованы эти волны?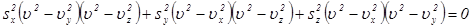 .
.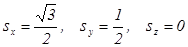 , получим два уравнения:
, получим два уравнения:
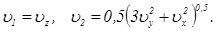
 , получим
, получим  . Обозначим амплитуду вектора
. Обозначим амплитуду вектора 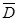 первой волны
первой волны 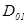 , второй -
, второй - 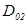 , тогда уравнения волн можно записать в виде
, тогда уравнения волн можно записать в виде ,
, - частота волны,
- частота волны, 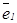 и
и 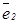 - единичные векторы, ортогональные
- единичные векторы, ортогональные 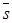 и определяющие поляризацию волн (см. рис. 12). Так как
и определяющие поляризацию волн (см. рис. 12). Так как  то, очевидно,
то, очевидно, 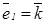 ,т.е. волна
,т.е. волна 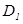 поляризована вдоль оси
поляризована вдоль оси 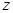 . Вектор
. Вектор 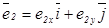 . Так как модуль вектора
. Так как модуль вектора 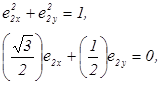
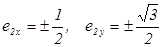 .
. вырезана из одноосного кристалла так, что оптическая ось параллельна плоскости пластины. На пластину нормально падает линейно поляризованная волна
вырезана из одноосного кристалла так, что оптическая ось параллельна плоскости пластины. На пластину нормально падает линейно поляризованная волна 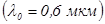 единичной интенсивности, плоскость колебаний которой составляет угол
единичной интенсивности, плоскость колебаний которой составляет угол 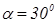 с оптической осью. Как будет поляризована волна на выходе, если показатели преломления для обыкновенной и необыкновенной волн равны соответственно
с оптической осью. Как будет поляризована волна на выходе, если показатели преломления для обыкновенной и необыкновенной волн равны соответственно 
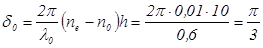 .
. , ось
, ось  которой совмещена с оптической осью. Так как
которой совмещена с оптической осью. Так как 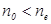 (кристалл положительный), то
(кристалл положительный), то 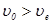 , а поскольку обыкновенная волна поляризована вдоль оси
, а поскольку обыкновенная волна поляризована вдоль оси 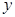 , то ось
, то ось 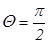 ) имеет вид
) имеет вид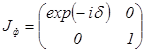 .
. ,
, ,
,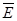 . Параметры эллипса поляризации предлагаем читателю определить самостоятельно (см. разд. 1).
. Параметры эллипса поляризации предлагаем читателю определить самостоятельно (см. разд. 1).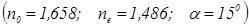 падает нормально к передней грани луч света. Найти угол между выходящими из призмы лучами.
падает нормально к передней грани луч света. Найти угол между выходящими из призмы лучами. и
и 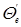 углы преломления обыкновенного и необыкновенного лучей, можно записать (углы падения
углы преломления обыкновенного и необыкновенного лучей, можно записать (углы падения  )
)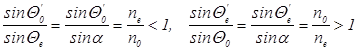 .
. и
и 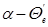 .Углы преломления
.Углы преломления  и
и  этих лучей найдем из закона преломления:
этих лучей найдем из закона преломления: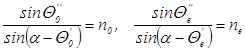 .
. ;
;  , поэтому угол между выходящими лучами
, поэтому угол между выходящими лучами  .
.


