Введем в рассмотрение вектор  . Поскольку для каждого направления
. Поскольку для каждого направления  в кристалле существуют две лучевые скорости
в кристалле существуют две лучевые скорости  и
и 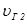 , определяемые уравнением (2.20), то вектор
, определяемые уравнением (2.20), то вектор 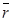 является двузначным по модулю. При изменении вектора
является двузначным по модулю. При изменении вектора  во всем пространстве конец вектора
во всем пространстве конец вектора 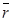 опишет некоторую двухоболочечную поверхность. Эта поверхность, являющаяся, по определению, годографом введенного вектора, называется лучевой поверхностью. Аналогичным образом можно ввести понятие волновой поверхности кристалла как годографа вектора
опишет некоторую двухоболочечную поверхность. Эта поверхность, являющаяся, по определению, годографом введенного вектора, называется лучевой поверхностью. Аналогичным образом можно ввести понятие волновой поверхности кристалла как годографа вектора 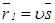 . В инженерной практике большее распространение получила первая из них, поэтому в дальнейшем мы ограничимся рассмотрением свойств и применением только лучевой поверхности.
. В инженерной практике большее распространение получила первая из них, поэтому в дальнейшем мы ограничимся рассмотрением свойств и применением только лучевой поверхности.
Рассмотрим кристалл, в котором для определенности положим  или
или  . Отметим, что в указанных неравенствах может быть использован лишь один из знаков равенства: в противном случае кристалл является изотропным и дальнейшие рассуждения теряют смысл.
. Отметим, что в указанных неравенствах может быть использован лишь один из знаков равенства: в противном случае кристалл является изотропным и дальнейшие рассуждения теряют смысл.
Рассмотрим вначале случай строгих неравенств. Для компонент и модуля введенного вектора 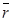 лучевой поверхности справедливы равенства
лучевой поверхности справедливы равенства
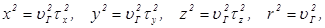
с учетом которых уравнение (2.20) приводится к виду
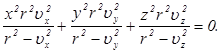
Освобождаясь от знаменателей, получим уравнение лучевой поверхности в виде
 . (2.23)
. (2.23)
Для выяснения вида лучевой поверхности рассмотрим сечения ее координатными плоскостями.
1. Плоскость  ,
,  . В этом случае
. В этом случае 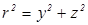 и уравнение (2.23) после несложных преобразований приводится к двум уравнениям
и уравнение (2.23) после несложных преобразований приводится к двум уравнениям
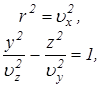
первое из которых есть уравнение окружности радиуса 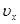 , второе - эллипс с полуосями
, второе - эллипс с полуосями 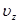 и
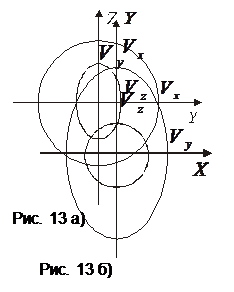
и 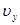 соответственно (рис. 13а).
соответственно (рис. 13а).
2. Плоскость  ,
,  . В этом случае
. В этом случае 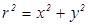 и уравнение (2.23) приводится к двум уравнениям вида
и уравнение (2.23) приводится к двум уравнениям вида
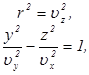
являющихся также уравнениями окружности радиуса 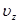 и эллипса с полуосями
и эллипса с полуосями 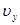 и
и 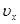 (рис. 13б).
(рис. 13б).

3. Плоскость
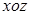
,

. В этой плоскости
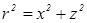
, и после преобразований (2.23) получим уравнения двух кривых
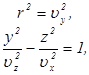 (2.24)
(2.24)
т.е. окружности радиуса 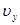 и эллипса с полуосями
и эллипса с полуосями 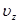 и
и 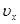 (рис. 13в). Эти кривые пересекаются в четырех точках, образующих два направления
(рис. 13в). Эти кривые пересекаются в четырех точках, образующих два направления  , названные ранее лучевыми оптическими осями кристалла. Эти направления образуют с осью
, названные ранее лучевыми оптическими осями кристалла. Эти направления образуют с осью 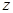 (ось соответствующей наименьшей главной скорости или наибольшей диэлектрической проницаемости) углы
(ось соответствующей наименьшей главной скорости или наибольшей диэлектрической проницаемости) углы  определяемые соотношениями
определяемые соотношениями
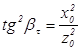 ,
,
где  и
и  - координаты точек пересечения. Из выражения (2.24) получим
- координаты точек пересечения. Из выражения (2.24) получим

следовательно,
 . (2.25)
. (2.25)
Таким образом, лучевые оптические оси кристалла параллельны координатной плоскости 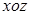 , т.е. плоскости, образованной осями, соответствующими максимальному и минимальному значениям диэлектрических проницаемостей кристалла. В этой жe плоскости, кстати, находятся и волновые оптические оси, причем можно показать, что
, т.е. плоскости, образованной осями, соответствующими максимальному и минимальному значениям диэлектрических проницаемостей кристалла. В этой жe плоскости, кстати, находятся и волновые оптические оси, причем можно показать, что
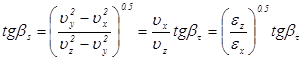 . (2.26)
. (2.26)
При  кристалл называют положительным, в противном случае - отрицательным.
кристалл называют положительным, в противном случае - отрицательным.
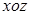 ,
,  . В этой плоскости
. В этой плоскости 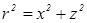 , и после преобразований (2.23) получим уравнения двух кривых
, и после преобразований (2.23) получим уравнения двух кривых

 . Поскольку для каждого направления
. Поскольку для каждого направления  в кристалле существуют две лучевые скорости
в кристалле существуют две лучевые скорости  и
и 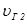 , определяемые уравнением (2.20), то вектор
, определяемые уравнением (2.20), то вектор 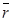 является двузначным по модулю. При изменении вектора
является двузначным по модулю. При изменении вектора 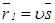 . В инженерной практике большее распространение получила первая из них, поэтому в дальнейшем мы ограничимся рассмотрением свойств и применением только лучевой поверхности.
. В инженерной практике большее распространение получила первая из них, поэтому в дальнейшем мы ограничимся рассмотрением свойств и применением только лучевой поверхности. или
или  . Отметим, что в указанных неравенствах может быть использован лишь один из знаков равенства: в противном случае кристалл является изотропным и дальнейшие рассуждения теряют смысл.
. Отметим, что в указанных неравенствах может быть использован лишь один из знаков равенства: в противном случае кристалл является изотропным и дальнейшие рассуждения теряют смысл.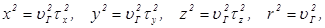
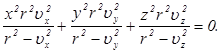
 . (2.23)
. (2.23) ,
,  . В этом случае
. В этом случае 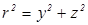 и уравнение (2.23) после несложных преобразований приводится к двум уравнениям
и уравнение (2.23) после несложных преобразований приводится к двум уравнениям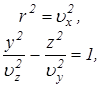
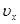 , второе - эллипс с полуосями
, второе - эллипс с полуосями 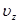 и
и 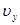 соответственно (рис. 13а).
соответственно (рис. 13а). ,
,  . В этом случае
. В этом случае 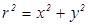 и уравнение (2.23) приводится к двум уравнениям вида
и уравнение (2.23) приводится к двум уравнениям вида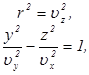

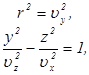 (2.24)
(2.24) , названные ранее лучевыми оптическими осями кристалла. Эти направления образуют с осью
, названные ранее лучевыми оптическими осями кристалла. Эти направления образуют с осью 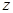 (ось соответствующей наименьшей главной скорости или наибольшей диэлектрической проницаемости) углы
(ось соответствующей наименьшей главной скорости или наибольшей диэлектрической проницаемости) углы  определяемые соотношениями
определяемые соотношениями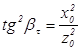 ,
, и
и  - координаты точек пересечения. Из выражения (2.24) получим
- координаты точек пересечения. Из выражения (2.24) получим
 . (2.25)
. (2.25)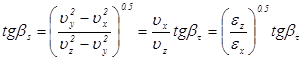 . (2.26)
. (2.26) кристалл называют положительным, в противном случае - отрицательным.
кристалл называют положительным, в противном случае - отрицательным.


