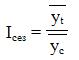Тема 7 .Статистическое изучение динамики социально-экономических явлений
Для выполнения задания по теме 7 используют данные о внутригодичной динамике пассажирооборота, приведенные в табл. 7.1.
На основании этих данных необходимо:
1. дать характеристику интенсивности изменения уровней ряда динамики, рассчитав показатели динамического ряда (по цепной и базисной схеме): абсолютные приросты, темпы роста, темпы прироста, абсолютные значения одного процента прироста;
2. охарактеризовать средний уровень и среднюю интенсивность внутригодичного развития показателя, рассчитав средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста;
3. дать характеристику тенденции в развитии явления механическим сглаживанием:
- по трехчленной ступенчатой средней;
- по трехчленной скользящей средней.
Фактические и сглаженные значения грузооборота изобразить графически;
4. охарактеризовать сезонность в динамике пассажирооборота; сезонные колебания изобразить графически.
Т а б л и ц а 7.1
Динамика объёма перевозок пассажиров, млн. пасс-км, в прямом сообщении
| Варианты
| Месяцы
| | Январь
| Февраль
| Март
| Апрель
| Май
| Июнь
| Июль
| Август
| Сентябрь
| Октябрь
| Ноябрь
| Декабрь
| |
|
|
|
|
|
|
|
|
|
|
|
|
| Требуется провести анализ динамики грузооборота за первое полугодие. Для удобства и наглядности исходные и рассчитанные показатели приведены в табличной форме (табл. 7.2).
Таблица 7.2.
Динамика объёма перевозок пассажиров, млн. пасс-км, в прямом сообщении
| Месяцы
| Грузооборот
| Абсолютный
прирост
(снижение)
по сравнению
| Темп роста,
%, по сравнению
| Темпы прироста, %, по сравнению
| Абсо-лютное значение 1%
прироста
| | с предыдущим периодом
| с янва-рем
| с предыдущим периодом
| с янва-рем
| с предыдущим периодом
| с янва-рем
| |
|
|
|
|
|
|
|
|
| | Январь
|
| -
| -
| -
| -
| -
| -
| -
| | Февраль
|
| -10
| -10
| 95,54
| 95,54
| -4,46
| -4,46
| 2,24
| | Март
|
|
|
| 138,32
| 132,14
| 38,32
| 32,14
| 2,14
| | Апрель
|
| -36
|
| 87,84
| 116,07
| -12,16
| 16,07
| 2,96
| | Май
|
| -23
|
| 91,15
| 105,80
| -8,85
| 5,80
| 2,6
| | Июнь
|
|
|
| 101,27
| 107,14
| 1,27
| 7,14
| 2,37
| | Июль
|
| -10
|
| 95,83
| 102,68
| -4,17
| 2,68
| 2,4
| | Август
|
| -18
| -12
| 92,17
| 94,64
| -7,83
| -5,36
| 2,3
| | Сентябрь
|
|
|
| 112,26
| 106,25
| 12,26
| 6,25
| 2,12
| | Октябрь
|
| -26
| -12
| 89,08
| 94,64
| -10,92
| -5,36
| 2,38
| | Ноябрь
|
| -8
| -20
| 96,23
| 91,07
| -3,77
| -8,93
| 2,12
| | Декабрь
|
|
|
| 110,78
| 100,89
| 10,78
| 0,89
| 2,04
| | Итого
|
|
| -
| -
| -
| -
| -
| -
| Абсолютный прирост (Δ Y) определяется как разность двух сравниваемых уровней:
Δ Y б = Yi – Y 0;Δ Y ц = Yi – Yi- 1,
где Yi – уровень i -го года;
Y 0 – уровень базисного года.
Таблица 7.3.
Динамика темпов прироста
|
| Абсолютный прирост по сравнению с предыдущим периодом
| Абсолютный прирост по сравнению с январем
| | ΔY Январь
| -
| -
| | ΔY Февраль
| 214-224=-10
| 214-224=-10
| | ΔY Март
| 296-214=82
| 296-224=72
| | ΔY Апрель
| 260-296=-36
| 260-224=36
| | ΔY Май
| 237-260=-23
| 237-224=13
| | ΔY Июнь
| 240-237=3
| 240-224=16
| | ΔY Июль
| 230-240=-10
| 230-224=6
| | ΔY Август
| 212-230=-18
| 212-224=-12
| | ΔY Сентябрь
| 238-212=26
| 238-224=14
| | ΔY Октябрь
| 212-238=-26
| 212-224=-12
| | ΔY Ноябрь
| 204-212=-8
| 204-224=-20
| | ΔY Декабрь
| 226-204=22
| 226-224=2
| Темп роста ( ) определяется отношением текущего уровня к базисному или предыдущему и выражается в процентах: ) определяется отношением текущего уровня к базисному или предыдущему и выражается в процентах:
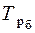  или или 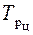  . .
Таблица 7.4.
Динамика темпов роста
|
| Темп роста, %
по сравнению с предыдущим периодом
| Темп роста, %
по сравнению с январем
| | Tp Январь
| -
| -
| | Tp Февраль
| (214/224)*100=95,54
| (214/224)*100=95,54
| | Tp Март
| 296/214*100=138,32
| 296/224*100=132,14
| | Tp Апрель
| 260/296*100=87,84
| 260/224*100=116,07
| | Tp Май
| 237/260*100=91,15
| 237/224*100=105,80
| | Tp Июнь
| 240/237*100=101,27
| 240/224*100=107,14
| | Tp Июль
| 230/240*100=95,83
| 230/224*100=102,68
| | Tp Август
| 212/230*100=92,17
| 212/224*100=94,64
| | Tp Сентябрь
| 238/212*100=112,26
| 238/224*100=106,25
| | Tp Октябрь
| 212/238*100=89,08
| 212/224*100=94,64
| | Tp Ноябрь
| 204/212*100=96,23
| 204/224*100=91,07
| | Tp Декабрь
| 226/204*100=110,78
| 226/224*100=100,89
| Темп прироста можно вычислить путем вычитания из темпов роста 100%, то есть Tпр = Tр – 100.
Таблица 7.5.
Динамика темпов прироста
|
| Темп прироста, %
по сравнению с предыдущим периодом
| Темп прироста, %
по сравнению с январем
| | Tпp Январь
| -
| -
| | Tпp Февраль
| 95,54-100=-4,46
| 95,54-100=-4,46
| | Tпp Март
| 138,32-100=38,32
| 132,14-100=32,14
| | Tпp Апрель
| 87,84-100=-12,16
| 116,07-100=16,07
| | Tпp Май
| 91,15-100=-8,85
| 105,80-100=5,80
| | Tпp Июнь
| 101,27-100=1,27
| 107,14-100=7,14
| | Tпp Июль
| 95,83-100=-4,17
| 102,68-100=2,68
| | Tпp Август
| 92,17-100=-7,83
| 94,64-100=-5,36
| | Tпp Сентябрь
| 112,26-100=12,26
| 106,25-100=6,25
| | Tпp Октябрь
| 89,08-100=-10,92
| 94,64-100=-5,36
| | Tпp Ноябрь
| 96,23-100=-3,77
| 91,07-100=-8,93
| | Tпp Декабрь
| 110,78-100=10,78
| 100,89-100=0,89
| Показатель абсолютного значения одного процента прироста (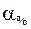 ) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах: ) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах:
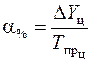 или или 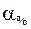 = 0,01· Yi– 1. = 0,01· Yi– 1.
Таблица 7.6.
Динамика темпов прироста
|
| Абсолютное значение 1% прироста
|  Январь Январь
| -
|  Февраль Февраль
| -10/-4,46=2,24
|  Март Март
| 82/32,14=2,14
|  Апрель Апрель
| -36/16,07=2,96
|  Май Май
| -23/5,8=2,6
|  Июнь Июнь
| 3/7,14=2,37
|  Июль Июль
| (-10)/2,68=2,4
|  Август Август
| (-18)/(-5,36)=2,3
|  Сентябрь Сентябрь
| 26/6,25=2,12
|  Октябрь Октябрь
| -26/(-5,36)=2,38
|  Ноябрь Ноябрь
| -8/(-8,93)=2,12
|  Декабрь Декабрь
| 22/0,89=2,04
| Средний уровень интервального ряда динамики с равноотстоящими интервалами рассчитывается по формуле средней арифметической простой:
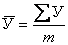 , ,
где m - число уровней в ряду.
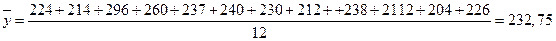
Средний абсолютный прирост – показатель, характеризующий среднюю абсолютную скорость роста (или снижения) уровня за отдельные периоды времени. Он показывает, на сколько единиц увеличился (или уменьшился) уровень сравнению с предыдущим в среднем за единицу времени – год, месяц и т.д. определяется по формуле:
 или или 
где У0 - начальный уровень ряда;
Уn - конечный уровень ряда;
m - число уровней в ряду;
n - номер конечного уровня ряда.
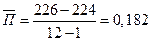
Средний темп роста в форме коэффициента рассчитывается только для цепных темпов роста по формуле средней геометрической простой:
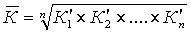
где К 'i - цепной коэффициент роста уровня ряда;
n – число цепных коэффициентов роста в ряду динамики.
или же исчисляется по формуле:
 , ,
где n= m – 1,
m - число уровней в ряду;
Средний темп роста в форме процента: 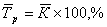
Средний темп прироста относительный показатель, выраженный в процентах, рассчитывается по формуле: 
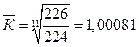 или 100,08% или 100,08%
Методы выявления основной тенденции ряда динамики
| месяцы
| Уровни ряда
| Способ ступенчатой средней
| Способ скользящей средней
| Индекс сезонности
| | Укрупненные интервалы
| Средняя хронологич.
| Подвижная трехлетняя сумма
| Скользящая средняя
| | Январь
|
|
| 244,67
|
| 244,67
| 105,66
| | Февраль
|
|
| 256,67
| 100,94
| | Март
|
|
| 264,33
| 139,62
| | Апрель
|
|
| 245,67
|
| 245,67
| 122,64
| | Май
|
|
| 235,67
| 111,79
| | Июнь
|
|
| 227,33
| 113,21
| | Июль
|
|
| 226,67
|
| 226,67
| 108,49
| | Август
|
|
| 220,67
| 100,00
| | Сентябрь
|
|
| 218,00
| 112,26
| | Октябрь
|
|
| 214,00
|
| 214,00
| 100,00
| | Ноябрь
|
| -
| -
| 96,23
| | Декабрь
|
| -
| -
| 106,60
| Средний уровень ряда равен 232,75
Метод скользящей средней заключается в следующем: формируются укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получаем, постепенно сдвигаясь от начального уровня ряда на один уровень. По укрупненным интервалам определяем среднюю из уровней, входящих в каждый интервал
Вместо относительных разностей за каждый месяц может быть вычислен индекс сезонности, который рассчитывается как отношение среднего уровня соответствующего месяца к общей средней. Индекс сезонности рассчитывается:
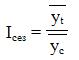
yt — средний уровень показателя соответствующего месяца за три и более лет,
yc — среднемесячное (по году) значение показателя за все годы (общая средняя).
Литература
Теория статистики / под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 2003.
Гусаров В.М. Теория статистики. – М.:Аудит, Издательское объединение «Юпити», 1998.
Статистика: курс лекций / под. ред. В.Г. Иванова. – Новосибирск, Инфра-М, 2000.
Злотницкая Т.С., Шабанова Т.В. Статистика. Часть 1: учебное пособие.- СПБГТУРП., – СПБ, 2009.
Рудаковая Р. Б., Бунин Л.Л., Гаврилов В.И. Практикум по статистике – СПб.: Питер, 2007.

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|

Логические цифровые микросхемы Более сложные элементы цифровой схемотехники (триггеры, мультиплексоры, декодеры и т.д.) не имеют...
|
Принципы, критерии и методы оценки и аттестации персонала
Аттестация персонала является одной их важнейших функций управления персоналом...
Пункты решения командира взвода на организацию боя. уяснение полученной задачи; оценка обстановки; принятие решения; проведение рекогносцировки; отдача боевого приказа; организация взаимодействия...
Что такое пропорции?
Это соотношение частей целого между собой. Что может являться частями в образе или в луке...
|
Лечебно-охранительный режим, его элементы и значение.
Терапевтическое воздействие на пациента подразумевает не только использование всех видов лечения, но и применение лечебно-охранительного режима – соблюдение условий поведения, способствующих выздоровлению...
Тема: Кинематика поступательного и вращательного движения. 1. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется со временем
1. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью...
Условия приобретения статуса индивидуального предпринимателя. В соответствии с п. 1 ст. 23 ГК РФ гражданин вправе заниматься предпринимательской деятельностью без образования юридического лица с момента государственной регистрации в качестве индивидуального предпринимателя. Каковы же условия такой регистрации и...
|
|

 ) определяется отношением текущего уровня к базисному или предыдущему и выражается в процентах:
) определяется отношением текущего уровня к базисному или предыдущему и выражается в процентах: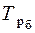
 или
или 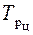
 .
.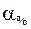 ) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах:
) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах: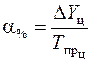 или
или  Январь
Январь
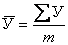 ,
,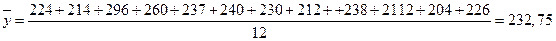
 или
или 
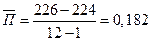
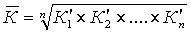
 ,
,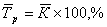

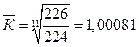 или 100,08%
или 100,08%