Построение правильных многоугольников по данной стороне

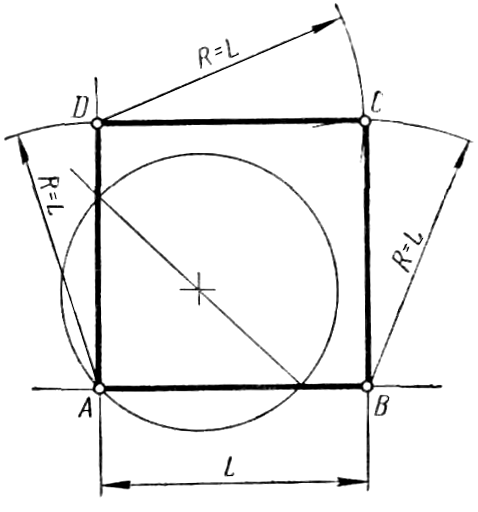
Построение квадрата по данной его стороне L (рисунок 34). На произвольной прямой откладывают отрезок AB, равный стороне квадрата L. Из любого конца отрезка, например из точки A, восстанавливают перпендикуляр и на нем откладывают отрезок AD = L. Затем из точек B и D как из центров проводят дуги радиусом R = L и на пересечении их отмечают точку С. Соединив прямыми точку C с точками B и D, получают квадрат с заданной стороной L.

Рисунок 34

 

Построение правильного шестиугольника по данной его сторонеL (рисунок 35). Известно, что сторона правильного шестиугольника равна радиусу окружности, описанной вокруг него. Поэтому, построив на произвольной прямой отрезок AB=L (рисунок 35, а), из концов его как из центров проводят две дуги радиусом R = L до взаимного пересечения их в точке О. Приняв точку О за центр, проводят окружность тем же радиусом R=L и делят ее на шесть равных частей. Точки деления являются вершинами правильного шестиугольника со стороной L (рисунок 35, б).

а б

Рисунок 35

 

Построение правильного шестиугольника с помощью линейки и угольника с углами 60 и 30° показано на рисунке 36.

 

Рисунок 36

 

Приближенный способ построения правильных многоугольников данной сторонеAB (рисунок 37).Изложенный ниже способ заключается в том, что правильный многоугольник строят как вписанный в окружность. Из концов отрезка АВ радиусом, равным этому отрезку, проводят две дуги до взаимного пересечения их в точках О и О₆. Из точек A и В к отрезку AB восстанавливают перпендикуляры, и на пересечении их с проведенными дугами получают две вершины квадрата (на рисунке 37 отмечена одна из них). Центр O₄ окружности, описанной около квадрата, расположен в точке пересечения диагонали квадрата с вертикальной прямой OO₆. Для построения вписанного пятиугольника отрезок O₄O₆ делят пополам в точке O₅ и из нее как из центра описывают окружность радиусом, равным отрезку O₅A. Сторона AB пять раз уложится на этой окружности. Центры окружностей, в которые сторона AB укладывается 8, 10, 12 и т. д. раз, расположены в точках пересечения прямой OO₆ с окружностями соответственно радиусов O₄A, О₅А, О₆А и т. д. Разделив пополам отрезки O₆O₈, O₈O₁₀, O₁₀O₁₂ и т.д., получают точки O₇, O₉, O₁₁ и т. д., являющиеся центрами окружностей, в которые сторона AB укладывается 7, 9, 11 и т. д. раз. Радиусы этих окружностей равны O₇A, O₉A, O₁₁A и т.д.

 

Рисунок 37