Деление окружности на равные части и построение правильных вписанных многоугольников

Для деления окружности пополам достаточно провести любой еедиаметр. Два взаимно перпендикулярных диаметра разделят окружность на четыре равные части (рисунок 28, а).Разделив каждую четвертую часть пополам, получают восьмые части, а при дальнейшем делении – шестнадцатые, тридцать вторые части и т. д. (рисунок 28, б).Если соединить прямымиточки деления, то можно получить стороны правильного вписанного квадрата(а₄), восьмиугольника (а₈) и т. д. (рисунок 28, в).

Рисунок 28

 

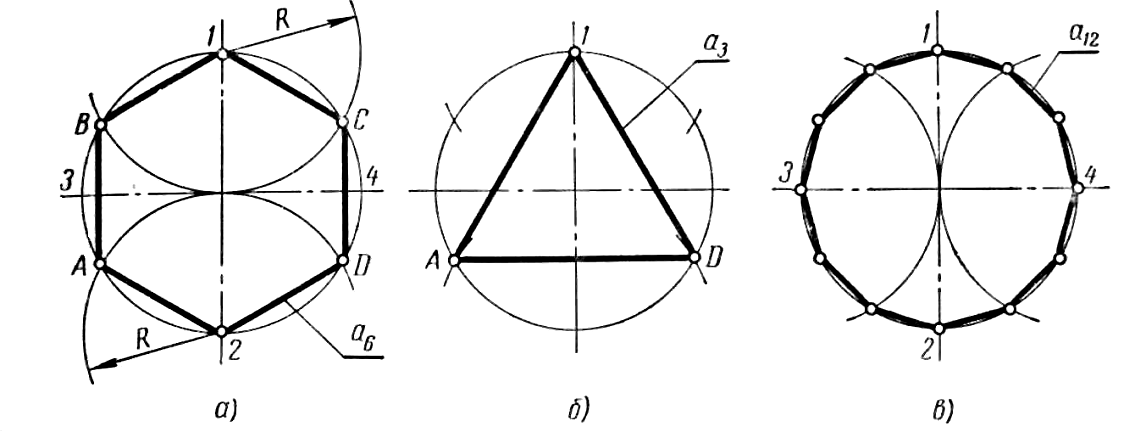
Деление окружности на 3, 6, 12 и т, д. равных частей, а также построение соответствующих правильных вписанных многоугольников осуществляют следующим образом. В окружности проводят два взаимно перпендикулярных диаметра 1–2 и 3–4 (рисунок 29 а). Из точек 1 и 2 как из центров описывают дуги радиусом окружности R до пересечения с ней в точках А, В, С и D. Точки A, B, 1, С, D и 2 делят окружность на шесть равных частей. Эти же точки, взятые через одну, разделят окружность на три равные части (рисунок 29, б). Для деления окружности на 12 равных частей описывают еще две дуги радиусом окружности из точек 3 и 4 (рисунок 29, в).

а б в

Рисунок 29

 

Построить правильные вписанные треугольник, шестиугольник и т. д. можно также с помощью линейки и угольника в 30 и 60°. На рисунке 30 приведено подобное построение для вписанного треугольника.

 

Рисунок 30

 

Деление окружности на семь равных частей и построение правильного вписанного семиугольника (рисунок 31) выполняют с помощью половины стороны вписанного треугольника, приблизительно равной стороне вписанного семиугольника.

Рисунок 31

 

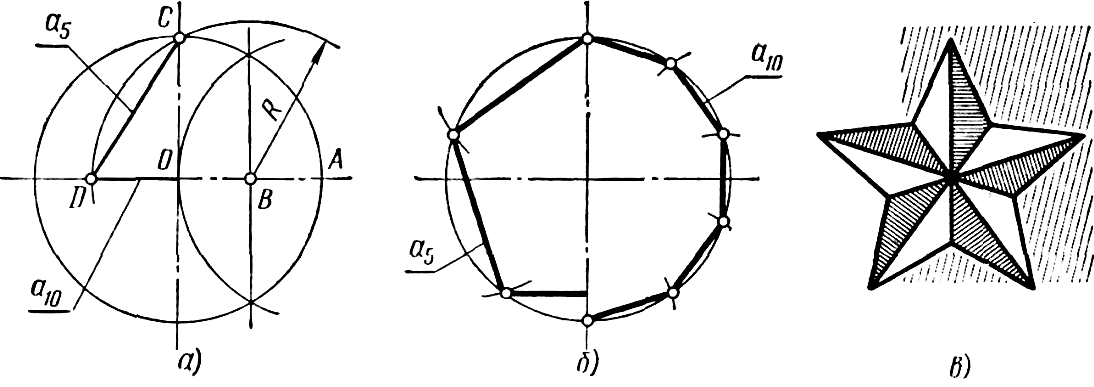
Для деления окружности на пять или десятьравных частей проводят два взаимно перпендикулярных диаметра (рисунок 32, а). Радиус OA делят пополам и, получив точку В, описывают из нее дугу радиусом R=BC до пересечения ее в точке D с горизонтальным диаметром. Расстояние между точками C и D равно длине стороны правильного вписанного пятиугольника (а₅), а отрезок OD равен длине стороны правильного вписанного десятиугольника (а₁₀). Деление окружности на пять и десять равных частей, а также построение вписанных правильных пятиугольника и десятиугольника показаны на рисунке 32, б. Примером использования деления окружности на пять частей является пятиконечная звезда (рисунок 32, в).

а б в

Рисунок 32

 

На рисунке 33 приведен общий способ приближенного деления окружности на равные части. Пусть требуется разделить окружность на девять равных частей. В окружности проводят два взаимно перпендикулярных диаметра и вертикальный диаметр AB делят на девять равных частей с помощью вспомогательной прямой (рисунок 33, а). Из точки B описывают дугу радиусом R = AB, и на пересечении ее с продолжением горизонтального диаметра получают точки С и D. Из точек C и D через четные или нечетные точки деления диаметра AB проводят лучи. Точки пересечения лучей с окружностью разделят ее на девять равных частей (рисунок 33, б).

Рисунок 33

 

При построении необходимо учитывать, что такой способ деления окружности на равные части требует особенно большой точности выполнения всех операций.