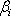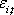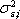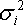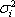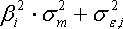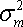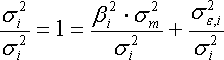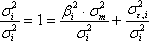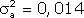*) Вычислены ранее без регрессионных формул
Оценка результатов регрессии. Вычисленные параметры 
и 
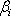
регрессионной модели дают представление об общих тенденциях взаимосвязей между изменениями доходности рыночного портфеля 
и доходностью 
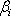
оцениваемой акции. Однако величины и не позволяют давать однозначный ответ о степени подобной взаимосвязи. Точность регрессионной модели, степень взаимосвязи и определяется разбросом случайных ошибок 
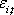
, который можно оценить с помощью дисперсии случайной ошибки 
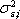
. Кроме того, точность регрессии можно определить, оценивая, сколь точно регрессионная модель определяет дисперсию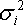 
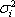
доходности ценных бумаг, для которых составляется регрессионная модель.
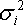
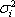
Чуть ниже будет показано, что дисперсию i-ой ценной бумаги можно представить в виде двух слагаемых:
= 
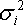
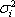
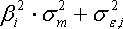
Как видим, первое слагаемое свидетельствует, что часть риска i-ой ценной бумаги определяется нестабильностью самого рынка, поскольку туда входит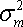 
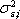
- дисперсия рыночной доходности r m. Второе же слагаемое показывает, что в суммарном риске ценной бумаги присутствует и собственная доля, не зависящая от колебаний рынка.
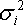
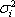
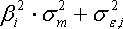
Разделим обе части равенства = на величину :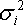
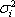
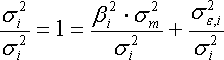
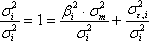
Обратим внимание, что в этом случае первое слагаемое будет показывать, какую долю в суммарном риске ценной бумаги можно описать с помощью регрессионной модели = 
, а второе слагаемое - степень неточности регрессионной модели. Значит, чем ближе величина 
к единице, тем более точная регрессионная модель.
- это квадрат коэффициента корреляции 
. Именно квадрат коэффициента корреляции является мерой оценки точности линейной регрессии, то есть мерой того, насколько точно уравнение регрессии подходит для описания соотношений реальных данных и .
Вычислим величину 
для акций "А";, "В"; и "С";, вспомнив ранее вычисленные значения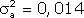 
; 
; 
:
Эти данные свидетельствуют, что лучше всего линейная регрессия описывает поведение акций компании "А";, так как величина 
ближе к единице, чем для других компаний. Для компании "С"; использование выбранного индекса РЦБ при составлении линейной регрессионной модели не оправданно, так как только 6% (0,0598) изменений ее доходности можно связать с колебаниями рынка.
