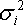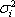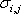Граница эффективных портфелей.

Выберем n акций, зададим два начальных условия:

а) длительность будущего холдингового периода;

б) количество N шагов расчета в прошлом.

 

После этого вычислим 3 необходимые характеристики каждой акции: , и . Зададим после этого произвольную комбинацию весов этих акций (их сумма должна равняться единице) и сформируем некий портфель K. Тогда по выведенным выше формулам можно вычислить ожидаемую доходность и стандартное отклонение этого портфеля. Возьмем координатную плоскость и отложим на ней эти значения. В итоге получим точку К на графике с координатами [ ; ] (рис. 8).

 

Рис. 8. Граница эффективных портфелей

 

Изменим веса выбранных n акций, получим уже другой портфель (например, портфель N), для которого также можно вычислить ожидаемую доходность и риск и отложить полученные значения на графике. В результате получим точку N.

Введем еще одно допущение модели Г. Марковица:

Допущение 6: Каждую акцию портфеля можно разделить на неограниченное число частей, и инвестор в состоянии приобрести любую часть акции. Иными словами, вес каждой акции портфеля может принимать любое значение. Это позволяет из ограниченного числа акций за счет изменения их весов формировать бесконечно много портфелей.

Если для каждого портфеля, созданного из выбранных n акций за счет комбинации их весов, определить ожидаемую доходность и стандартное отклонение, отложить их величины на графике, то получим совокупность точек - область существования портфелей, определяющую все возможные портфели для выбранного количества ценных бумаг. Эта зона имеет характерное "зонтикообразное" очертание. В зависимости от количества и характеристик ценных бумаг, входящих в портфель (ожидаемые доходности, дисперсии, ковариации) эта зона может смещаться влево-вправо или вверх-вниз, поворачиваться, становиться более пологой или крутой.

Теорема о существовании эффективного множества. Задача инвестора – сформировать из n выбранных акций единственный оптимальный портфель, обеспечивающий этому инвестору максимальную полезность. Ключ к решению проблемы выбора оптимального портфеля лежит в сформулированной Г. Марковицем теореме о существовании эффективного набора портфелей, так называемой границы эффективных портфелей.

Суть теоремы сводится к выводу о том, что любой инвестор должен выбрать из всего бесконечного набора портфелей, сформированных на базе n акций, такой портфель, который удовлетворяет одному из двух (но не двум сразу!) условий:

1) Обеспечивает максимальную ожидаемую доходность при каждом выбранном уровне риска;

2) Обеспечивает минимальный риск для каждой выбранной величины ожидаемой доходности.

 

Портфели, удовлетворяющие этим условиям, Марковиц относит к эффективным портфелям.

Фактически, суть теоремы Марковица сводится к следующему: если инвестор выбрал n акций, по известным алгоритмам вычислил необходимые характеристики [ ; ; ] для каждой акции портфеля, а затем произвольно задал какое-то значение ожидаемой доходности портфеля = Е*, то найдется только одна комбинация ценных бумаг в портфеле, минимизирующая риск портфеля при заданном значении доходности Е*.

Набор портфелей, которые минимизируют уровень риска при каждой величине ожидаемой доходности, образует так называемое эффективное множество. Если отобразить эффективное множество на координатной плоскости, то получим границу эффективных портфелей (ГЭП) - на рисунке ГЭП совпадает с левой границей области существования портфелей.