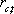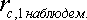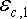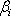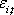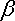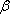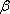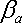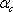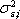В таком случае для акции С уравнение линейной регрессии должно принимать вид:


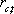
 =
= 



Ниже будут вычислены параметры линейной регрессии для акции С: 


 =0,1165 и
=0,1165 и 


 =0,5255. Значит, для этой акции уравнение линейной регрессии должно иметь вид:
=0,5255. Значит, для этой акции уравнение линейной регрессии должно иметь вид:


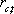
 = 0,1165 + 0,5256×
= 0,1165 + 0,5256× 



Сравним получаемые по этой формуле теоретические величины 

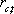
 и реально наблюдаемые значения
и реально наблюдаемые значения 

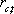
 , приведенные в таблице 7:
, приведенные в таблице 7:



 = 0,1165 + 0,5256×
= 0,1165 + 0,5256× 


 = 0,1165 + 0,5256×0,121 = 0,1802,
= 0,1165 + 0,5256×0,121 = 0,1802,
что отличается от наблюдаемого значения 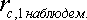


 = 0,110. Чтобы уровнять теоретическую и реальную величины, необходимо провести коррекцию теоретической величины
= 0,110. Чтобы уровнять теоретическую и реальную величины, необходимо провести коррекцию теоретической величины 


 . Достигается это путем добавления к значению
. Достигается это путем добавления к значению 


 ошибки
ошибки 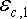


 = -0,0702: (0,1802 - 0,0702 = 0,110).
= -0,0702: (0,1802 - 0,0702 = 0,110).
Поскольку величины 


 и
и 

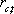
 случайные, то, скорее всего, и остальные теоретические значения
случайные, то, скорее всего, и остальные теоретические значения 

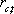
 , получаемые с использованием уравнения линейной регрессии, будут отличаться от реально наблюдаемых величин
, получаемые с использованием уравнения линейной регрессии, будут отличаться от реально наблюдаемых величин 

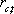
 , приведенных в таблице 7. В этой связи величины
, приведенных в таблице 7. В этой связи величины 


 необходимо корректировать ошибкой
необходимо корректировать ошибкой 


 на каждом шаге расчета. Так как величины
на каждом шаге расчета. Так как величины 


 и
и 

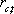
 случайные, то и значения ошибки
случайные, то и значения ошибки 


 также должны представлять собой случайные величины. В итоге уравнение линейной регрессии для акции С должно иметь следующий вид:
также должны представлять собой случайные величины. В итоге уравнение линейной регрессии для акции С должно иметь следующий вид:


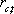
 =
= 


 +
+ 


 ,
,
где:



 - случайная ошибка.
- случайная ошибка.
В общем случае, если в портфель включено n акций, то для любой i -ой акции портфеля уравнение линейной регрессии выглядит следующим образом:



 =
= 


 ,
,
где:



 - доходность i -ой акции портфеля за шаг t;
- доходность i -ой акции портфеля за шаг t;



 - параметр регрессии, называемый коэффициентом «альфа»; показывает, какая часть доходности i -ой акции портфеля не связана с изменениями доходности рыночного портфеля
- параметр регрессии, называемый коэффициентом «альфа»; показывает, какая часть доходности i -ой акции портфеля не связана с изменениями доходности рыночного портфеля 


 ;
;


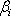
 - параметр линейной регрессии, называемый коэффициентом "бета";, показывающий чувствительность доходности i -ой акции портфеля к изменениям рыночной доходности
- параметр линейной регрессии, называемый коэффициентом "бета";, показывающий чувствительность доходности i -ой акции портфеля к изменениям рыночной доходности 


 ;
;



 - доходность рыночного портфеля в момент t;
- доходность рыночного портфеля в момент t;



 - случайная ошибка, свидетельствующая о том, что реальные, действующие значения
- случайная ошибка, свидетельствующая о том, что реальные, действующие значения 


 и
и 


 отклоняются от линейной зависимости.
отклоняются от линейной зависимости.
Уравнение 


 =
= 


 является основным в линейном регрессионном анализе и берется за основу в модели Шарпа. В линейном регрессионном анализе полагается, что средняя арифметическая (ожидаемая) величина ошибок наблюдения E (
является основным в линейном регрессионном анализе и берется за основу в модели Шарпа. В линейном регрессионном анализе полагается, что средняя арифметическая (ожидаемая) величина ошибок наблюдения E (

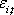
 )=0, то есть фактические величины
)=0, то есть фактические величины 


 в среднем равномерно распределяются выше и ниже значений, получаемых при линейной регрессии.
в среднем равномерно распределяются выше и ниже значений, получаемых при линейной регрессии.
Параметр бета. Особое значение необходимо уделить параметру 

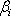
 , поскольку он определяет чувствительность доходности i-ой акции портфеля к изменениям рыночной доходности. Коэффициент
, поскольку он определяет чувствительность доходности i-ой акции портфеля к изменениям рыночной доходности. Коэффициент 

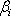
 для каждой ценной бумаги показывает, на сколько процентов изменится доля
для каждой ценной бумаги показывает, на сколько процентов изменится доля 


 , определяемая воздействием рынка (
, определяемая воздействием рынка (

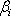
 ×
× 


 ), при изменении рыночной доходности на 1%.
), при изменении рыночной доходности на 1%.
В общем случае, если 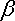

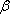
 >1, то доходность данной ценной бумаги более чувствительная, подвержена большим колебаниям, чем рыночная доходность r m. Соответственно, при
>1, то доходность данной ценной бумаги более чувствительная, подвержена большим колебаниям, чем рыночная доходность r m. Соответственно, при 

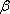
 <1 ценная бумага имеет меньший размах отклонений доходностей r j от средней арифметической (ожидаемой) величины E (ri), чем рыночная доходность. В этой связи ценные бумаги с коэффициентом
<1 ценная бумага имеет меньший размах отклонений доходностей r j от средней арифметической (ожидаемой) величины E (ri), чем рыночная доходность. В этой связи ценные бумаги с коэффициентом 

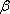
 >1 классифицируются как более рискованные, чем рынок в целом, а с
>1 классифицируются как более рискованные, чем рынок в целом, а с 

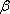
 <1 - менее рискованными, чем рынок в целом.
<1 - менее рискованными, чем рынок в целом.
Как показывают исследования, для большинства ценных бумаг коэффициент 

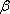
 >0, хотя могут встретиться ценные бумаги и с отрицательной величиной
>0, хотя могут встретиться ценные бумаги и с отрицательной величиной 

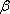
 . В последнем случае доходности этих ценных бумаг отрицательно коррелированны с доходностью рыночного портфеля. Следует учитывать, что и в случае отрицательных величин
. В последнем случае доходности этих ценных бумаг отрицательно коррелированны с доходностью рыночного портфеля. Следует учитывать, что и в случае отрицательных величин 

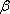
 , если величина этого коэффициента по модулю превосходит единицу, то есть
, если величина этого коэффициента по модулю превосходит единицу, то есть 


 (например,
(например, 

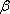
 = -1,5), то акции считаются более рискованными, чем рынок в целом.
= -1,5), то акции считаются более рискованными, чем рынок в целом.
Поскольку коэффициент 

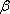
 характеризует зависимость доходности исследуемой акции и рыночного портфеля, то, очевидно, что данный коэффициент отражает только систематическую, недиверсифицируемую часть риска.
характеризует зависимость доходности исследуемой акции и рыночного портфеля, то, очевидно, что данный коэффициент отражает только систематическую, недиверсифицируемую часть риска.
Определение параметров 


 и
и 

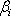
 регрессионной модели и оценка результатов регрессии. Для нахождения параметров
регрессионной модели и оценка результатов регрессии. Для нахождения параметров 


 и
и 

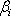
 по результатам наблюдений используется метод наименьших квадратов (МНК). По этому методу в качестве параметров
по результатам наблюдений используется метод наименьших квадратов (МНК). По этому методу в качестве параметров 


 и
и 

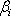
 берутся такие значения, которые минимизируют сумму квадратов ошибок
берутся такие значения, которые минимизируют сумму квадратов ошибок 

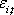
 , то есть которых величина:
, то есть которых величина:




достигает минимума. Если провести необходимые вычисления, то окажется, что выражение имеет минимум, когда параметры 


 и
и 

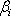
 принимают следующие значения:
принимают следующие значения:








Если будут известны наблюдаемые в течение N лет величины 


 и
и 


 , то, пользуясь известными формулами для вычисления ожидаемых доходностей, ковариаций и дисперсий, можно найти E (r i), E (r m),
, то, пользуясь известными формулами для вычисления ожидаемых доходностей, ковариаций и дисперсий, можно найти E (r i), E (r m), 


 и
и 


 , подставить их в выше представленные формулы и вычислить параметры регрессии
, подставить их в выше представленные формулы и вычислить параметры регрессии 


 и
и 

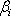
 .
.
Найдем значения коэффициентов 


 и
и 

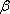
 для акций "А", "В" и "С":
для акций "А", "В" и "С":



 =0,2494 и
=0,2494 и 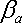


 = -0,9787
= -0,9787



 = -0,0117 и
= -0,0117 и 


 =0,9470
=0,9470


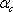
 = 0,1165 и
= 0,1165 и 


 = 0,5256
= 0,5256
Вычисление дисперсий случайной ошибки. Поскольку для определения оптимального портфеля с использованием модели Шарпа понадобятся значения дисперсий 

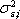
 случайных ошибок, то проведем необходимые вычисления. Общая формула для вычисления дисперсии случайной ошибки имеет вид:
случайных ошибок, то проведем необходимые вычисления. Общая формула для вычисления дисперсии случайной ошибки имеет вид:


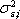
 =
= 



Для акций "А" вычисления дают:



 = [(0,120-0,2694+0,9787×0,1212)
= [(0,120-0,2694+0,9787×0,1212) 


 +(-0,040-0,2694+0,9787×0,2924)
+(-0,040-0,2694+0,9787×0,2924) 


 +(0,010×0,2694+0,9787×0,1479)
+(0,010×0,2694+0,9787×0,1479) 


 +
+
+ и т.д. по всем 10 годам] / 8 = 0,0073
Соответственно: 


 =0,0136 и
=0,0136 и 


 =0,0375.
=0,0375.
Для наглядности сведем данные регрессионного анализа для акций "А", "В" и "С" в одну таблицу (табл. 8.):
Таблица 8.