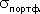Ожидаемая доходность
портфеля   
|
0,1208
|
0,1300
|
0,1400
|
0,1500
|
0,1600
|
0,1700
|
0,1940
|
Стандартное
отклонение  
|
0,0440
|
0,0500
|
0,0654
|
0,0857
|
0,1081
|
0,1316
|
0,1894
|
Если перенести вычисленные значения ожидаемой доходности и стандартного отклонения эффективных портфелей, сформированные на основе акций компаний "А";, "В"; и "С";, на координатную плоскость, обвести полученные точки, то получим линию – границу эффективных портфелей (рис. 9.):
Рис. 9. Граница эффективных портфелей в соответствии в полученными данными
Как видно из рисунка 9, заданной величине риска портфеля, положим, s* соответствуют два эффективных портфеля 1 и 2. Однако, согласно теореме Г. Марковица инвестор должен предпочесть портфель 2. Аналогично инвестор поступит и при иных величинах 
. Тогда очевидно, что инвестору вообще не имеет смысла строить нижнюю ветвь границы эффективных портфелей (ГЭП), расположенную ниже точки R. Портфель R соответствует портфелю с минимальной дисперсией. (MVP). В этой связи при построении ГЭП рекомендуется предварительно вычислить характеристики MVP, а затем при вычислении величин весов акций подставлять Е*≥ E(rMVP). На рисунке граница эффективных портфелей проходит через точку MVP, соответствующую портфелю с минимальной дисперсией.
Находить веса MVP можно следующим способом: в исходной матрице Т вычеркнуть строку и столбец, соответствующие ограничению Е* (в нашем случае это четвертая строка и четвертый столбец), и для полученной матрицы (Т – 1) найти матрицу 
, обратную матрице (T –? 1). Коэффициенты в первых трех строках последнего столбца этой обратной матрицы составят веса портфеля с минимальной дисперсией. Для акций компаний "А", "В" и "С" эти веса будут равны: WА = 0,5195; WВ = 0,4077; WС = 0,0727.
Нахождение оптимального портфеля. Как отмечалось, в теории Марковица инвесторы стремятся сформировать портфель ценных бумаг, чтобы максимизировать получаемую полезность. Иными словами, каждый инвестор желает таким образом сформировать портфель, чтобы сочетание ожидаемой доходности 
и уровня риска портфеля приносило ему максимальное удовлетворение потребностей и минимизировало риск при желаемой доходности. Разные инвесторы имеют отличные друг от друга мнения об оптимальности сочетания и , поскольку отношение одного инвестора к риску не похоже на желание рисковать другого инвестора. Поэтому, говоря об оптимальном портфеле, надо иметь в виду, что эта категория сугубо индивидуальна, и оптимальные портфели разных инвесторов теоретически отличаются друг от друга. Тем не менее, каждый оптимальный портфель непременно является эффективным, то есть инвесторы выбирают удовлетворяющий их (оптимальный) портфель из эффективных портфелей.
Метод определения оптимального портфеля основывается на совмещении объективно полученной границы эффективных портфелей и субъективной оценки отдельным инвестором полезности того или иного портфеля, то есть той или иной комбинации 
и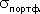 
. Построив границу эффективных портфелей, инвестор должен задать сам себе вопрос какую доходность он ожидает от портфеля? Предположим, что таковой является = 0,15. После этого по кривой границы эффективных портфелей он определяет уровень риска такого портфеля: 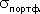=0,0857. Затем инвестор должен оценить, удовлетворяет ли его такой уровень риска. Если инвестор готов к более высокому уровню риска, то ему целесообразно выбрать портфель с =0,16 и 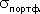=0,1081. Тот портфель, который при установленной инвестором доходности даст наилучшее сочетание и , будет оптимальным.
