Значение доходности акций трех фирм за 10 шагов расчета
Вычислим ожидаемые (средние арифметические) доходности акций наших трех фирм:
или 10,5%;
Аналогичные вычисления для акций "Веги" и "Сириуса" дают:
Измерение риска отдельной акции портфеля. Доходность оцениваемой акции за будущий холдинговый период равняется ожидаемой доходности
Поскольку ожидаемая доходность акции
Вычислим дисперсии и стандартные отклонения доходностей акций наших трех фирм:
Аналогичные вычисления для двух других акций дают:
При оценке инвестиционной привлекательности акций следует предпочесть ту из них, которая обеспечивает более высокую ожидаемую доходность и меньший уровень риска. Однако на практике более доходные акции часто имеют и более высокий уровень риска. В этом случае инвестиционный выбор можно сделать с использованием коэффициента отклонения CV:
показывающего, какая доля риска приходится на один процент ожидаемой доходности. Предпочесть следует ту акцию, которая имеет наименьшее значение CV.
Для наших акций получаются следующие значения:
То есть предпочесть следует акцию С.
Измерение доходности и риска портфеля. Чтобы найти доходность и риск всего портфеля инвестору, прежде всего, необходимо определить, какую долю из имеющейся у него на момент t суммы денег Sначальн. он направит на приобретение той или иной акции портфеля. Предположим, что инвестор располагает суммой Sначальн. =10 тыс. рублей и решает сумму Sa направить на приобретение акции А, а сумму Sb – на покупку акции В. Принято долю:
направленную на приобретение акций "А", называть весом акции А в портфеле. Соответственно
Очевидно, что если в портфель включено n акций, то сумма весов всех акций портфеля должна равняться единице:
Доходность портфеля. Пусть в портфель объединяются n акций. На инвестиционной терминологии данная фраза означает, что в портфель включены акции n эмитентов. Так, если в формируемый портфель будет включено 10 акций фирмы «А», 20 акций «В» и 30 акций «С», то считается, что такой портфель содержит 3 акции. Алгебраически под ожидаемой доходностью портфеля понимается средневзвешенное значение ожидаемых величин доходности акций, входящих в портфель:
где:
n - число акций в портфеле.
Если инвестор решит сформировать портфель из акций трех компаний и разделить начальный капитал между ними в пропорции: Wa =0,1; Wb =0,35; Wc =0,55, то:
E(ra+b+c) =0,1×0,105+0,35×0,128+0,55×0,194=0,162
Измерение риска портфеля. Риск портфеля оценивается с помощью дисперсии его доходности В статистике меру взаимозависимости двух случайных величин измеряют с помощью ковариации и коэффициента корреляции. Если оценивается ковариация si,j доходностей акций i и j портфеля за N шагов расчета, то ковариация подсчитывается по формуле:
где: ri,t и rj,t - наблюдаемые доходности ценных бумаг i и j в момент времени t; E(ri), E(rj) - ожидаемые доходности ценных бумаг; N - общее количество шагов наблюдений. Высчитаем ковариации между доходностями акций "А", "В" и "С":
= 1/9× [(0,120?0,105)×(?0,080?0,128)+(?0,040?0,105)×(0,240?0,128)+ (0,010?0,105)×(0,210?0,128) + (0,330?0,105)×(?0,020?0,128) + + (0,100?0,105)×(0,130?0,128) + (0,270?0,105)×(?0,030?0,128) + (0,090?0,105)×(0,200?0,128) + (?0,010?0,105)×(0,340?0,128) + + (0,130?0,105)×(0,220?0,128) + (0,050?0,105)×(0,070?0,128)]=?0,012.
Аналогичные вычисления дают: sa,c = -0,006; sb,c = +0,006 Часто при определении степени взаимосвязи двух случайных величин используют относительную величину - коэффициент корреляции ρi,j:
Значения В общем виде дисперсия портфеля, состоящего из n ценных бумаг, выражается формулой:
Если вспомнить, что коэффициент корреляции
Предположим для примера, что инвестор формирует портфель из трех ценных бумаг акций компаний "А";, "В"; и "С";. При этом из имеющейся у него первоначальной суммы инвестиций он тратит Wa = 0,2 на акции "А", Wb = 0,3? на акции фирмы "В"; и Wc = 0,5?на акции "С";. Чему равен риск и ожидаемая доходность E (r n ) такого портфеля? Проведем вычисления, используя ранее полученные величины:
E(rn) = Wa×E(ra)+Wb×E(rb)+Wc×E(rc) = 0,2×0,105+0,3×0,128+0,5×0,194 = 0,156 или 15,6%.
=0,04×0,014+0,09×0,019+0,025×0,036+2×0,2×0,3×(?0,012)+2×0,2×0,5×(?0,006)+2×0,3×0,5×0,006=0,0104
|



















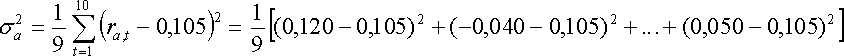










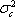






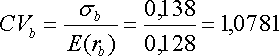






























 и
и 

















