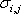Соотношение риска и доходности портфеля.

Допущение 5. В своих теоретических исследованиях Марковиц полагал, что значения доходности акций портфеля являются случайными величинами, распределенными по нормальному (Гауссовскому) закону. В этом случае для исчерпывающей характеристики любого портфеля достаточно оценивать лишь два показателя: - ожидаемую доходность и - стандартное отклонение как меру риска.

Формула дисперсии портфеля содержит две части: первая часть включает только квадраты величин и всегда положительная. Во вторую часть входят ковариации . Ковариации могут быть отрицательными. Поэтому варьируя состав портфеля за счет изменения:

а) эмитентов акций (при неизменном количестве n акций в портфеле);

б) количества n акций в портфеле;

в) весов акций в портфеле

можно воздействовать на риск всего портфеля.

Процесс изменения содержимого портфеля путями а), б), в) с целью снижения риска портфеля называется диверсификацией портфеля. Диверсификация воздействует на риск портфеля и делит его на две части: та часть риска портфеля, которая может быть устранена путем диверсификации, называется диверсифицируемым, или несистематическим риском. Доля же риска, которая не устраняется диверсификацией, носит название недиверсифицируемого, или систематического риска.

Когда в портфель войдут все ценные бумаги, обращающиеся на финансовом рынке, то будет сформирован так называемый рыночный портфель. Риск рыночного портфеля практически полностью является систематическим. Это предельно низкий уровень риска, которого можно достичь за счет диверсификации управляемого портфеля.