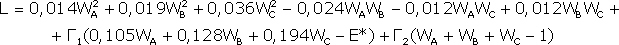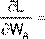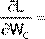Общая постановка задачи нахождения границы эффективных портфелей.

Подход Г. Марковица к нахождению оптимального портфеля следующий: пусть имеются n акций, из которых формируется портфель (в нашем примере n = 3). Зададим любое произвольное значение ожидаемой доходности портфеля = Е* , например, Е* = 0,14. Тогда задача инвестора сводится к следующему: из всего бесконечного набора портфелей с ожидаемой доходностью портфеля = 0,14,необходимо найти такой, который обеспечивал бы минимальный уровень риска.

Иными словами, можно задачу инвестора свести к следующему:

необходимо найти минимальное значение дисперсии портфеля

 

 

при заданных начальных условиях:

 

=

 

 

Существует 3 способа решения подобного рода задач - графический, математический и с использованием компьютерных программ. Далее будет рассмотрен математический метод оптимизации портфеля, наиболее полно отражающий ее сущность.

Математический способ. Для вычисления требуемых величин W _А, W _В и W _С используются множители Лагранжа. Рассмотрим последовательность действий в этом методе на примере акций "А", "В" и "С". Подставим вычисленные ранее значения , и для доходностей этих акций в выражения риска портфеля и доходности портфеля. Тогда задача сводится к следующей? необходимо найти минимальное значение величины:

 

 

при следующих начальных условиях:

 

Для решения этой задачи составляется полином Лагранжа L:

 

 

(Г₁ и Г ₂ в этом полиноме называются множителями Лагранжа).

 

После этого вычисляются частные производные полинома по каждой неизвестной величине W_А,W_В,W_С, Г₁, Г₂ и приравниваются нулю:

0,028W_А? 0,024W_В? 0,012W_С + 0,105Г₁ + Г₂ = 0

? 0,024W_А + 0,038W_В + 0,012W_С + 0,128Г₁ + Г₂ = 0

?0,012W_А + 0,012W_В + 0,072W_С + 0,194Г₁ + Г₂ = 0

0,105W_А + 0,128W_В + 0,194W_С - E* = 0

W_А + W_В + W_С?1 = 0

 

В матричной форме эти уравнения представляются в виде:

 

 

Если обозначить первую матрицу как T, вторую – как W, а третью – как E, то можно это равенство записать в виде матричного уравнения: T×W=E. Чтобы найти значения матрицы W необходимо определить матрицу , являющуюся обратной матрице T. Тогда: W = ×E. Для определения существуют специальные компьютерные программы, хотя это можно сделать и самостоятельно. Вычислив все члены матрицы и умножив матрицу на матрицу E, получим выражения для W_А,W_В,W_С:

 

W_А =?6,82337×E* + 1,344214

W_В =?5,9503×E* + 1,126742

W_С = + 12,77367×E* 1,47096

 

Задавая различные значения E* и вычисляя каждый раз по формулам представленным выше величины W_i, можно таким образом найти эффективные портфели и определить в каждом случае их дисперсии и стандартные отклонения.

Ниже в таблице 6 приведены значения ожидаемой доходности и стандартного отклонения для эффективных портфелей, составленных из акций компаний:

Таблица 6.