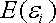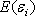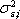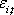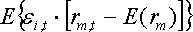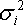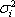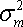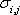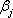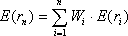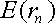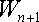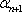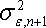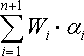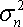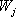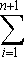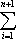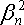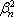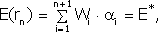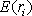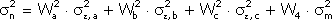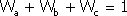Использование модели Шарпа для построения границы эффективных портфелей.

В основу модели Шарпа положена линейная регрессия. Для применения модели Шарпа необходимо предварительно ввести ряд условий. Если предположить, что инвестор формирует портфель из n ценных бумаг, то будем считать, что:

1) Средняя арифметическая (ожидаемая) величина случайных ошибок = 0 для всех акций портфеля, то есть для i=1,2,..., n.

2) Дисперсия случайных ошибок для каждой ценной бумаги постоянна.

3) Для каждой акции портфеля отсутствует корреляция между наблюдаемыми в течение N шагов расчета величинами случайных ошибок, то есть E [ × ]= 0 (t =1,2,..., N).

4) Отсутствует корреляция между случайными ошибками любых двух ценных бумаг в портфеле, иначе говоря, E [ × ]=0.

5) Отсутствует корреляция между случайными ошибками и рыночной доходности, то есть = 0.

Определение доходности и риска отдельной акции портфеля. Используя эти упрощения, можно получить выражения E (r _i), и s_i,j для любых акций в портфеле:

 

= + ×

= × +

= × ×

 

необходимые для построения границы эффективных портфелей. При этом инвестору требуется предварительно вычислить n значений , n величин , n значений , а также и . Следовательно, всего потребуется найти: (n + n + n +2)=3 n +2 начальных данных, что существенно меньше объема вычислений для модели Марковица. Например, при формировании портфеля из 30 ценных бумаг для определения границы эффективных портфелей надо 3×30+2=92 начальных данных по модели Шарпа и 495 (в 5 раз больше!) по модели Марковица.

Сокращение объема вычислений в модели Шарпа происходит потому, что все парные ковариации между доходностями ценных бумаг в портфеле предполагаются равными нулю. А чтобы отразить взаимное влияние риска одной ценной бумаги на риск другой ценной бумаги, Шарп предложил свести эти ковариационные эффекты к взаимосвязи ценных бумаг портфеля с каким-то рыночным индексом, например, S&P500. Иначе говоря, корреляция между доходностями ценных бумаг в портфеле выражается с помощью рыночного индекса.

Определение ожидаемой доходности и дисперсии портфеля. Как установлено, ожидаемая доходность портфеля, состоящего из n ценных бумаг, вычисляется по формуле:

 

 

где - вес каждой ценной бумаги в портфеле. Подставим в эту формулу выражение из формулы = + × :

 

= ×[ + × ]

 

Выделим в этом равенстве слагаемые, на которые не оказывает воздействие изменения рынка, и которые зависят от рыночных показателей:

 

= × + ( × )×

 

Для придания этой формуле компактности, Шарп предложил считать рыночный портфель в качестве условной (n +1)-ой акции портфеля. В таком случае, второе слагаемое уравнения = × + ( × )× можно представить в виде:

 

( × )× = × ( ), где:

= ×

( ) =

 

При этом считается, что дисперсия (n +1)-ой ошибки равна дисперсии рыночной доходности: = . Выражение = × представляет собой сумму взвешенных величин "беты" ( ) каждой ценной бумаги (где весом служат ) и называется портфельной бетой ( ).

С учетом выражений учетом выше сказанного формулу ожидаемой доходности портфеля можно записать так:

 

=

 

Итак, ожидаемую доходность портфеля E (rn) можно представить состоящей из двух частей:

а) суммы взвешенных параметров каждой ценной бумаги – W ₁a₁+ W ₂a₂+...+ W_n a _n, что отражает вклад в E (rn) самих ценных бумаг, и

б) компоненты W_{n +1}×a _{n +1}=( × )× , то есть произведения портфельной беты и ожидаемой рыночной доходности, что отражает взаимосвязь рынка с ценными бумагами портфеля.

Дисперсия портфеля. Как известно, дисперсию портфеля можно представить в виде:

 

= × + × ×

 

Если вместо значений и подставить сюда выражения:

 

= × +

= × ×

 

провести соответствующие вычисления и воспользоваться условиями (n+1) акции, то можно показать, что дисперсия портфеля представляется в виде:

 

= ×

 

При этом только необходимо иметь в виду, что W_{n +1} = × , то есть (W_{n +1}) =(W ₁×b₁+ W ₂×b₂+...+ W_n ×b _n) , а = . Значит, дисперсию портфеля, содержащего n акций, можно представить состоящей из двух компонент:

а) средневзвешенных дисперсий ошибок × , где весами служат , что отражает долю риска портфеля, связанного с риском самих ценных бумаг (собственный риск);

б) × - взвешенной величины дисперсии доходности рыночного портфеля , где весом служит квадрат портфельной беты, что отражает долю риска портфеля, определяемого нестабильностью самого рынка (рыночный риск).

 

Исходя из изложенного, можно аналогично тому, как это делалось в предыдущей части, показать, что с увеличением числа ценных бумаг в портфеле первая часть риска портфеля ( × ) будет стремиться к нулю. Поэтому диверсификация портфеля приводит к уменьшению риска, связанного с нестабильностью самих ценных бумаг, оставляя лишь компоненту × , зависящую от нестабильности самого рынка.

Формулирование цели инвестора в модели Шарпа. В модели Шарпа цель инвестора сводится к следующему:

необходимо найти минимальное значение дисперсии портфеля:

 

 

при следующих начальных условиях:

 

 

Отметим основные этапы, которые необходимо выполнить для построения границы эффективных портфелей в модели Шарпа:

1) Выбрать n ценных бумаг, из которых формируется портфель, и определить исторический промежуток в N лет, за который будут наблюдаться значения доходности каждой ценной бумаги.

2) По рыночному индексу (например, РТС) вычислить рыночные доходности для того же промежутка времени.

3) Найти величины и :

= - ×

 

4) Вычислить дисперсии ошибок регрессионной модели.

5) Решить с применением методов линейной алгебры задачу построения границы эффективных портфелей.

 

Рассмотрим пример построения границы эффективных портфелей, состоящих из акций "А";, "В"; и "С";. Итак, задача инвестора в этом случае сводится к следующему: необходимо минимизировать выражение:

 

 

при следующих начальных условиях:

 

 

Подставим вычисленные ранее значения , ,