План оформления доски
 Образец записи в тетрадях
Образец записи в тетрадях
План урока
1. Орг момент
2. Устный счет
3. Объяснение новой темы
4. Первичное закрепление
5. Повторение пройденного материала
6. Подведение итогов
7. Домашнее задание
| Этапы урока
| Ход урока
| Примечание
|
| Орг. момент
| Добрый день, ребята. Сегодня урок математики у вас буду вести я. Меня зовут Анна Алексеевна. Уберите со своих парт все лишнее, поправьтесь, улыбнитесь. Все готовы! Здравствуйте, садитесь.
|
|
| Устный счет
| Начнем наш урок с устного счета.
Задание 1.
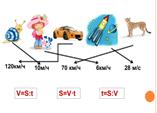
Ребята, посмотрите на доску. В первой колонке изображены движущиеся объекты, а во второй их скорости. Соотнесите движущийся объект и скорость
| Улитка
| 70 км/ч
| | Человек
| 28 м/с
| | Машина
| 10 м/ч
| | Ракета
| 120 км/ч
| | Гепард
| 6 км/ч
| Ответы:
| Улитка
| 10 м/ч
| | Человек
| 6 км/ч
| | Машина
| 120 км/ч
| | Ракета
| 28 м/с
| | Гепард
| 70 км/ч
|
А кто помнит, как найти скорость?
V=S:t
Посмотрите на схему, которая у нас получилась, и устно составьте задачу на нахождение пути. Но сначала вспомним формулу нахождения пути
S=V·t
Составьте обратную задачу. Но прежде вспомним формулу нахождения времени
t=S:V
Задание 2.
А теперь давайте решим устно задачу. Слушайте внимательно условие!
(Задача 58)
Буратино и Незнайка пошли в школу в 8 ч 30 мин. У школы они встретились. Буратино шел до встречи с Незнайкой 12 мин. Сколько минут был в пути Незнайка?
Ребята, кто решил задачу? Поднимите руку. Почему ты так решил (а)?
Ответ:12 минут, т. к. ребята вышли в одно время и встретились в одно время у школы.
Вывод: если 2 человека вышли в одно время и встретились одновременно, то с какой бы скоростью они не шли, время, затраченное на путь, одинаковое.
Задание 3.
Сколько всего единиц в 52 дес., 520 дес., 36 сот., 36 дес., 360 дес.
Ответ: 520, 5200, 3600, 360, 3600
Сколько всего единиц, десятков, сотен в числе 5486.
Ответ: 5486 единиц, 548 десятков, 54 сотни.
Задание 4.
А теперь мы решим устно примеры.
24*20 =480
Сначала 24 умножим на 2, потом на 10
25*30 =750
Сначала 25 умножим на 3, потом на 10
34*20 =680
Сначала 34 умножим на 20, потом на 10
15*40 =600
Сначала 15 умножим на 4, потом на 10
80*10 =800
Чем похожи все эти выражения? (умножаются на круглые числа)
|




|
| Объяснение новой темы
| А сейчас мы решим примеры, где оба множителя оканчиваются нулями. Откройте тетрадь, запишите число, классная работа, отступите 2 клетки вниз и запишите 80·40
- Как умножим 80 на 40?
(сначала умножим на 4, потом на 10).
Значит надо 80 умножить на 4, но 80 – это сколько десятков?
(8 десятков)
Значит, удобнее сначала 8 десятков умножить на 4. Сколько получится?
(32 десятка)
Теперь 32 десятка умножим на 10. Как это сделали? (Приписали справа один нуль)
Получилось 320 десятков. Как узнать, сколько единиц 320 десятках?
(Приписать справа нуль, получится 3200)
Сколько нулей мы записали в конце произведения? (Два. Первый мы приписали, когда умножали на 10, а второй, когда десятки выражали в единицах.) Обратите внимание, что в конце произведения записано столько нулей, сколько записано в конце обоих множителей вместе.
Рассмотрим второй пример. Отступите от предыдущего примера две клетки вниз и запишите 600*90
Как умножили 600 на 90?
(сначала умножили на 9, потом на 10).
Значит надо 600 умножить на 9, но 600 это сколько сотен?
(6 сотен)
Значит, удобнее сначала 6 сотен умножить на 9. Сколько получится?
(54 сотни)
Теперь 54 сотни умножим на 10. Как это сделали? (Приписали справа один нуль)
Получилось 540 сотен. Как узнать, сколько единиц 540 сотнях?
(Приписать справа два нуля, получится 54000) Сколько нулей мы записали в конце произведения? (Три. Первый мы приписали, когда умножали на 10, а еще два, когда десятки выражали в единицах.) Обратите внимание, что в конце произведения записано столько нулей, сколько записано в конце обоих множителей вместе.
В случае, когда устно трудно найти произведение двух чисел оканчивающиеся нулями, вычисления выполняют письменно. Посмотрим на запись в учебнике на странице 12.
Отступите 2 клетки вниз и запишите 7600*40
Пример 1
Надо найти произведение 7600 и 40. Обратите внимание на то, что второй множитель подписали под первым так, чтобы его цифра, отличная от нуля, стояла под первой цифрой справа первого множителя, отличного от нуля. Тогда нули обоих множителей будут записаны справа. Умножим сначала 76 сотен на 4, а результат умножим на 10. Для этого умножим 76 на 4. 6 умножим на 4, получим 24, 4 записываем под 6, а 2 запоминаем. Теперь 7 умножим на 4, получим 28, да еще 2, получается 30, запишем. Чему равно произведение 76 сотен и 4? (304 сотни) Теперь 304 сотни умножим на 10, получим 3040 сотен. Как их выразить в единицах? (приписать справа два нуля) Получилось 304000.
Сколько нулей в первом множители?
(два нуля)
А во втором?
(один нуль)
Сколько всего нулей записано в конце произведения? (три, т. е. столько, сколько их в обоих множителях.)
Пример 2
Отступите 3 клетки вправо и запишите.
Теперь разберем следующий пример.
Надо найти произведение 2540 и 300. Обратите внимание на то, что второй множитель подписали под первым так, чтобы его цифра, отличная от нуля, стояла под первой цифрой справа первого множителя, отличного от нуля.
Тогда нули обоих множителей будут записаны справа. Умножим сначала 254 десятка на 3, а результат умножим на 100. Для этого умножим 254 на 6. 4 умножим на 3, получим 12, 2 записываем под 4, а 1 запоминаем. Теперь 5 умножим на 3, получим 15, да еще 1, получается 16, запишем 6 под 5, а 1 запомним. Теперь 2 умножим на 3, получим 6, да еще 1, получается 7, запишем 7 под 2. Чему равно произведение 254 десятков и 3? (762 десятка) Теперь 762 десятка умножим на 100, получим 76200 десятка. Как их выразить в единицах? (приписать справа нуль) Получилось 762000. Сколько всего нулей записано в конце произведения? (три, т. е. столько, сколько их в обоих множителях.)
Пример 3
Отступите 3 клетки вправо и запишите.
Теперь разберем следующий пример.
К доске выйдет … и решит пример с объяснением.
Надо найти произведение 1720 и 60?
Как записываются эти два множителя?
Что умножим сначала?
Сколько получилось?
Что дальше?
Как их выразить в единицах?
(приписать справа нуль)
Получилось 103200.
Сколько нулей в первом множителе? Во втором?
Сколько всего нулей записано в конце произведения? (два, т. е. столько, сколько их в обоих множителях.)
Вывод: чтобы умножить два числа, оканчивающиеся нулями, нужно сначала умножать не обращая внимания на нули, а потом приписать столько нулей, сколько в обоих множителях.
| Дети открывают тетрадь
Ребенок выходит к доске.
Садится на место.
|
| Первичное закрепление нового
| Теперь сделаем № 55.
Первые 4 примера решаем на доске, а последние каждый в тетради с последующей проверкой.
4200*90 =378000
42 сотни сначала умножим на 9, а потом на 10. Выразим в единицах.
640*500 =32000
64 десятка сначала умножим на 5, а потом на 100. Выразим в единицах.
23480*30 =704400
2348 десятков умножим на 3, а потом на 10. Выразим в единицах.
7810*700 =5467000
781 десяток умножим на 7, а потом на 100. Выразим в единицах.
6290*800 =5032000
629 десятков умножим на 8, а потом на 100. Выразим в единицах.
43400*200 =8680000
434 сотни умножим на 2, а потом на 100. Выразим в единицах.
Что объединяет все эти выражения?
(умножались числа, оканчивающиеся нулями)
Как умножали?
(Сначала не обращая внимания на нули, а потом приписали столько нулей, сколько в обоих множителях)
Молодцы, ребята. Вы справились с заданием.
|
Ребенок выходит к доске.
Садится на место.
Ребенок выходит к доске.
Садится на место.
Ребенок выходит к доске.
Садится на место.
Ребенок выходит к доске.
Садится на место.
Ребенок выходит к доске.
Садится на место.
Ребенок выходит к доске.
Садится на место.
|
| Повторение пройденного материала
| А теперь решим задачу 57.
Зачитываю задачу.
От двух пристаней отправились навстречу друг другу два теплохода. Один из них шел до встречи 4 ч со средней скоростью 36 км/ч. Другой теплоход прошел до встречи третью часть пути, пройденного первым.
Поставь вопрос и реши задачу.
А теперь давайте сделаем чертеж.
(Сама составляю или вызываю ребенка?)
Начертите отрезок длинной 8 см.
Что сказано про пройденный путь первого теплохода?
А второго?
Значит пройденный путь первого, больше в 3 раза чем второго. Отмерьте 6 см от левого края и поставьте флажок.
Сколько часов был в пути 1 теплоход?
Разделите на чертеже пройденный путь 1го теплохода на 4 равные части.
Какой вопрос можно поставить к этой задаче?
1) сколько км прошел второй теплоход.
Какая скорость у первого теплохода?
(36км/ч)
Сколько времени он был в пути?
(4 часа)
Что мы можем узнать по этим данным?
(Пройденный путь первого теплохода)
Каким действием?
(Умножением)
Что мы знаем про пройденный путь второго теплохода?
(то, что он прошел третью часть пути, пройденного первым)
Мы можем узнать путь второго теплохода?
(да)
Каким действием?
(делением)
Ответ: 48 км прошел второй теплоход
2) Найдите скорость второго теплохода.
Какая скорость у первого теплохода?
(36км/ч)
Сколько времени он был в пути?
(4 часа)
Что мы можем узнать по этим данным?
(Пройденный путь первого теплохода)
Каким действием?
(Умножением)
Что мы знаем про пройденный путь второго теплохода?
(то, что он прошел третью часть пути, пройденного первым)
Мы можем узнать путь второго теплохода?
(да)
Каким действием?
(делением)
Мы знаем время второго теплохода?
(да, 4 часа)
Почему вы так решили?
(Два теплохода вышли одновременно и встретились в одно время. Значит, второй теплоход шел столько же, сколько и первый.)
Зная время и пройденный путь второго теплохода, мы может ответить на вопрос?
(да)
Каким действием?
(делением)
Ответ: 16 км/ч скорость второго теплохода.
3) Расстояние между двумя пристанями
Какая скорость у первого теплохода?
(36км/ч)
Сколько времени он был в пути?
(4 часа)
Что мы можем узнать по этим данным?
(Пройденный путь первого теплохода)
Каким действием?
(Умножением)
Что мы знаем про пройденный путь второго теплохода?
(то, что он прошел третью часть пути, пройденного первым)
Мы можем узнать путь второго теплохода?
(да)
Каким действием?
(делением)
Зная пройденный путь первого и второго теплохода, мы можем ответить на вопрос задачи?
(да)
Каким действием?
(сложением)
Что нужно знать, чтобы ответить на вопрос задачи?
- пройденный путь 1го и 2го теплоходов.
Каким действием?
- сложением
Ответ: 192 км расстояние между двумя пристанями.
|
Составляем чертеж
Ребенок выходит к доске.
Садится на место.
Ребенок выходит к доске.
Садится на место.
Ребенок выходит к доске.
Садится на место.
|
| Решение уравнений
| Сейчас мы с вами решим уравнения. Один ребенок выходит к доске.
1) Произведение неизвестного числа и числа 9 равно разности чисел 120 и 66.
х·9=120-66
х- это первый множитель
9 – это второй множитель
Произведение выражено разностью 120 и 66. Сразу решить уравнение мы не можем. Сначала надо найти разность. Произведение чисел х и 9 равно 54
х·9=54
х-это первый множитель.
Чтобы найти первый множитель нужно произведение разделить на второй множитель.
х=6
Проверим:
6·9=120-66
54=54
2) Частное неизвестного числа и числа 8 равно сумме чисел 320 и 80
х:8=320+80
х-это делимое
8 – это делитель
Частное выражено в виде суммы 320 и 80.
Сразу решить уравнение мы не можем. Сначала надо найти частное. Частное х и 8 равно 400.
х:8=400
х-это делимое. Чтобы найти делимое нужно частное умножить на делитель.
х=3200
Проверим:
3200:8=320+80
400=400
|
Ребенок выходит к доске.
Садится на место.
Ребенок выходит к доске.
Садится на место.
|
|
| Если останется время
Посмотрите номер 61.
Первый вариант самостоятельно решает первую строчку, а второй вторую.
I вариант
8 см2 25 мм2 = 825 мм2
30 а = 3000 м2
2400 а=24 га
II вариант
9 дм2 18 см2 = 918 см2
85 га = 8500 а
3800 м2 = 38 а
|
|
| Подведение итогов
| Ребята, что мы узнали сегодня на уроке?
(письменный прием умножения)
Кто расскажет, как нужно умножать?
(Сначала умножаем не обращая внимания на нули, а потом приписываем столько нулей, сколько в обоих множителях.)
|
|
|
| На дом вам номер 56 и 59.
Посмотрите номер 56. Как вы будете его делать?
Обратите внимание на выражение 70·9000, как удобнее его решать?
|
|
|
| Наш урок подошел к концу. До свидания.
|
|
Вариант № 0.
Задание 1. Найти пределы функций.
а) 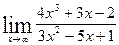 ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию 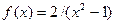 и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а)  ; б)
; б) 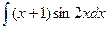 ;
;
в)  ; г)
; г) 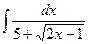 .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б)  .
.
Задание 6. Найти обшее решение дифференциального уравнения
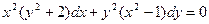 и частное решение,
и частное решение,
удовлетворяющее начальным условиям х0=0, у0=0.
Задание 7. Написать три первых члена ряда по заданному общему члену
 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и
исследовать сходимость ряда на концах интервала.
Вариант № 1.
Задание 1. Найти пределы функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию  и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а) 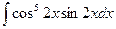 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б)  .
.
Задание 6. Найти общее решение дифференциального уравнения
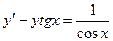 и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
удовлетворяющее начальным условиям х0=0, у0=0,  .
.
Задание 7. Написать три первых члена ряда по заданному общему члену
 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и
исследовать сходимость ряда на концах интервала.
Вариант № 2.
Задание 1. Найти пределы функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а) 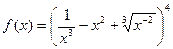 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию  и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б)  .
.
Задание 6. Найти общее решение дифференциального уравнения
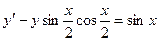 и частное решение,
и частное решение,
удовлетворяющее начальным условиям х0=p/2, у0=0.
Задание 7. Написать три первых члена ряда по заданному общему члену
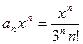 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и
исследовать сходимость ряда на концах интервала.
Вариант № 3.
Задание 1. Найти пределы функций.
а)  ; б)
; б) 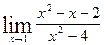 ;
;
в)  ; г)
; г)  ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г) 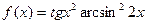 .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию  и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а) 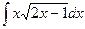 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б) 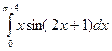 .
.
Задание 6. Найти общее решение дифференциального уравнения
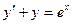 и частное решение,
и частное решение,
удовлетворяющее начальным условиям х0=0, у0=  .
.
Задание 7. Написать три первых члена ряда по заданному общему члену
 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и
исследовать сходимость ряда на концах интервала.
Вариант № 4.
Задание 1. Найти пределы функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а) 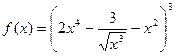 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию  и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б)  .
.
Задание 6. Найти общее решение дифференциального уравнения
 и частное решение,
и частное решение,
удовлетворяющее начальным условиям х0=0, у0=0.
Задание 7. Написать три первых члена ряда по заданному общему члену
 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и
исследовать сходимость ряда на концах интервала.
Вариант № 5.
Задание 1. Найти пределы функций.
а) 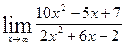 ; б)
; б) 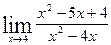 ;
;
в)  ; г)
; г)  ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г) 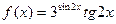 .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию  и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а)  ; б)
; б) 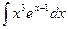 ;
;
в)  ; г)
; г)  .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 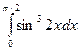 ; б)
; б) 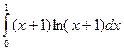 .
.
Задание 6. Найти общее решение дифференциального уравнения
 и частное решение,
и частное решение,
удовлетворяющее начальным условиям х0=0, у0=0.
Задание 7. Написать три первых члена ряда по заданному общему члену
 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и
исследовать сходимость ряда на концах интервала.
Вариант № 6.
Задание 1. Найти пределы функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию 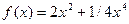 и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 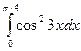 ; б)
; б)  .
.
Задание 6. Найти общее решение дифференциального уравнения
 и частное решение,
и частное решение,
удовлетворяющее начальным условиям х0=0, у0=0  .
.
Задание 7. Написать три первых члена ряда по заданному общему члену 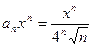 , определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала.
, определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала.
Вариант № 7.
Задание 1. Найти пределы функций.
а)  ; б)
; б)  ;
;
в) 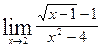 ; г)
; г) 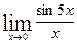 ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а)  ; б)
; б)  ;
;
в) 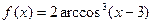 ; г)
; г)  .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию  и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а)  ; б)
; б) 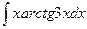 ;
;
в)  ; г)
; г) 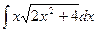 .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б)  .
.
Задание 6. Найти общее решение дифференциального уравнения
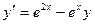 и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
удовлетворяющее начальным условиям х0=0, у0=0 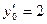 .
.
Задание 7. Написать три первых члена ряда по заданному общему члену  , определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала.
, определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала.
Вариант № 8.
Задание 1. Найти пределы функций.
а)  ; б)
; б)  ;
;
в) 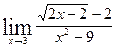 ; г)
; г) 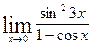 ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а)  ; б)
; б)  ;
;
в)  ; г))
; г))  .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию  и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а) 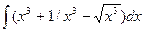 ; б)
; б) 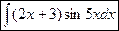 ;
;
в)  ; г)
; г)  .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б) 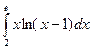 .
.
Задание 6. Найти общее решение дифференциального уравнения
 и частное решение,
и частное решение,
удовлетворяющее начальным условиям х0=1, у0=0.
Задание 7. Написать три первых члена ряда по заданному общему члену
 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и
исследовать сходимость ряда на концах интервала.
Вариант № 9.
Задание 1. Найти пределы функций.
а)  ; б)
; б) 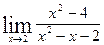 ;
;
в)  ; г)
; г)  ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию  и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а) 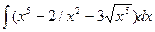 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 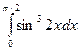 ; б)
; б)  .
.
Задание 6. Найти общее решение дифференциального уравнения
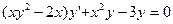 и частное решение,
и частное решение,
удовлетворяющее начальным условиям х0=0, у0=1.
Задание 7. Написать три первых члена ряда по заданному общему члену
 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и
исследовать сходимость ряда на концах интервала.
Вариант № 0.
Задание 1. Найти пределы функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию  и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б)  .
.
Задание 6. Найти обшее решение дифференциального уравнения
 и частное решение,
и частное решение,
удовлетворяющее начальным условиям х0=0, у0=0.
Задание 7. Написать три первых члена ряда по заданному общему члену
 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и
исследовать сходимость ряда на концах интервала.
Вариант № 1.
Задание 1. Найти пределы функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию  и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б)  .
.
Задание 6. Найти общее решение дифференциального уравнения
 и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
удовлетворяющее начальным условиям х0=0, у0=0,  .
.
Задание 7. Написать три первых члена ряда по заданному общему члену
 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и
исследовать сходимость ряда на концах интервала.
Вариант № 2.
Задание 1. Найти пределы функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 3. Исследовать средствами дифференциального исчисления
функцию  и построить ее график.
и построить ее график.
Задание 4. Найти неопределенные интегралы.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задание 5. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б)  .
.
Задание 6. Найти общее решение дифференциального уравнения
 и частное решение,
и частное решение,
удовлетворяющее начальным условиям х0=p/2, у0=0.
Задание 7. Написать три первых члена ряда по заданному общему члену
 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и
исследовать сходимость ряда на концах интервала.
Вариант № 3.
Задание 1. Найти пределы функций.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  .
.
Задание 2. Найти производные заданных функций.
а)  ; б)
; б)  ;
;









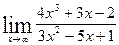 ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
.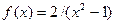 и построить ее график.
и построить ее график. ; б)
; б) 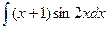 ;
; ; г)
; г) 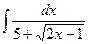 .
. ; б)
; б)  .
.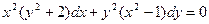 и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график.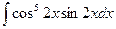 ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
.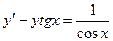 и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
и частное решение, удовлетворяющее начальным условиям х0=0, у0=0. .
. , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
.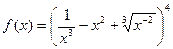 ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
.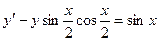 и частное решение,
и частное решение,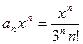 , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б) 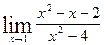 ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г) 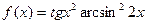 .
. и построить ее график.
и построить ее график.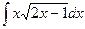 ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б) 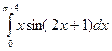 .
.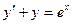 и частное решение,
и частное решение, .
. , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
.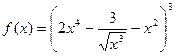 ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и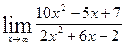 ; б)
; б) 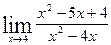 ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г) 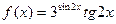 .
. и построить ее график.
и построить ее график. ; б)
; б) 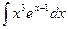 ;
; ; г)
; г)  .
.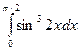 ; б)
; б) 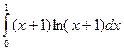 .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
.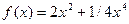 и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
.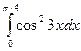 ; б)
; б)  .
. и частное решение,
и частное решение,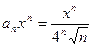 , определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала.
, определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала. ; б)
; б)  ;
;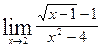 ; г)
; г) 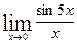 ;
; .
. ; б)
; б)  ;
;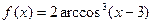 ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б) 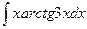 ;
; ; г)
; г) 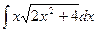 .
. ; б)
; б)  .
.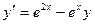 и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.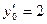 .
. , определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала.
, определить интервал сходимости ряда и исследовать сходимость ряда на концах интервала. ; б)
; б)  ;
;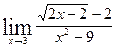 ; г)
; г) 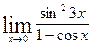 ;
; .
. ; б)
; б)  ;
; ; г))
; г))  .
. и построить ее график.
и построить ее график.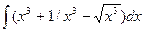 ; б)
; б) 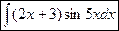 ;
; ; г)
; г)  .
. ; б)
; б) 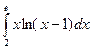 .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б) 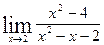 ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график.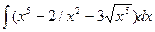 ; б)
; б)  ;
; ; г)
; г)  .
. .
.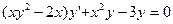 и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение, удовлетворяющее начальным условиям х0=0, у0=0.
и частное решение, удовлетворяющее начальным условиям х0=0, у0=0. .
. , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
; ; г)
; г)  .
. и построить ее график.
и построить ее график. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. и частное решение,
и частное решение, , определить интервал сходимости ряда и
, определить интервал сходимости ряда и ; б)
; б)  ;
; ; г)
; г)  ;
; .
. ; б)
; б)  ;
;


