Знаходження кута між прямою та площиною.
Якщо пряма l не перпендикулярна до площини π, то кутом між прямою та площиною називається кут між прямою цією прямою та її проекцією на дану площину.
Якщо у прямокутній декартовій системі координат задана площина π рівнянням Ах + By + Cz + D = 0, а пряма l канонічними рівняннями Синус кута між прямою l та площиною π знаходиться за формулою sin j Пряма l і площина π будуть паралельними тоді і тільки тоді, коли нормальний вектор площини і направляючий вектор прямої перпендикулярні, тобто їх скалярний добуток А для того щоб пряма l була перпендикулярна до площини π;, необхідно і достатньо, щоб ранг матриці Питання для самоперевірки. 1. Які ви знаєте способи задання прямої у просторі? 2. Що називається направляючим вектором прямої? 3. Як знайти відстань від точки до прямої? 4. За якою формулою ми можемо знайти відстань між двома 5. Назвіть умови, за яких дві прямі мимобіжні. 6. Скласти векторні параметричні рівняння прямої, яка задана в просторі точкою і направляючим вектором. 7. Вивести канонічні та параметричні рівняння прямої в просторі і рівняння прямої, яка проходить через дві задані точки. 8. Написати загальні рівняння прямої. Як перейти від загальних рівнянь прямої до канонічних? 9. Як знайти кут між двома прямими в просторі? Написати умови паралельності і перпендикулярності прямих. 10. Як визначити взаємне розташування площини та прямої, що задана точкою та направляючим вектором (канонічними рівняннями)? 11. Як знайти кут між прямою та площиною? Які умови паралельності і перпендикулярності прямої і площини? 12. Довести, що умову, за якої дві прямі 13. Довести, що рівняння площини, яка проходить через пряму
|


 , тоді нормальним вектором площини p буде вектор
, тоді нормальним вектором площини p буде вектор  (А, В, С), направляючим вектором прямої l – вектор
(А, В, С), направляючим вектором прямої l – вектор  (т, п, р).
(т, п, р).
 або
або  = 0.
= 0. був рівний одиниці, тобто
був рівний одиниці, тобто  .
. і
і 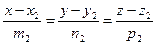 лежать в одній площині, можна записати у вигляді:
лежать в одній площині, можна записати у вигляді: 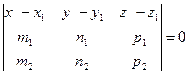 .
.


