Взаємне розташування двох прямих у просторі.
Тема №36. Деятельность следователя по профилактике преступлений
План:
Введение.
1. Понятие и общая характеристика профилактической деятельности в органах внутренних дел.
2. Направления профилактической деятельности следователя.
Заключение.
Нехай задано дві прямі l1 та l2, які визначаються відповідно: l1 – точкою M1 (x1, y1, z1) і направляючим вектором 1.
2. 3. Паралельні:
4. Перетинаються: мішаний добуток векторів ( Інакше взаємне розташування двох прямих у просторі можна визначити за допомогою рангів матриць. Розглянемо матриці 1. Прямі l1 та l2 мимобіжні тоді і лише тоді, коли R = 3; 2. Прямі l1 та l2 перетинаються тоді і лише тоді, коли R = r = 2; 3. Прямі l1 та l2 паралельні тоді і лише тоді, коли R = 2, r = 1; 4. Прямі l1 та l2 співпадають тоді і лише тоді, коли R = r = 1. Знаходження відстані від точки до прямої.
Якщо у прямокутній декартовій системі координат пряма l задана точкою M1(x1, y1, z1) та направляючим вектором  (α, β, γ), тоді відстань від точки М0 (х0 , у0 , z0) до даної прямої знаходиться як висота паралелограма по формулі:
Знаходження відстані між двома мимобіжними прямими. Якщо у прямокутній декартовій системі координат дано дві мимобіжні прямі рівняннями (l1):
|
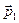(α1, β1, γ1) і l2 – точкою M2 (x2, y2, z2) і направляючим вектором 
(α2, β2, γ2). Можливі слідуючи випадки розташування прямих:
Мимобіжні: тоді мішаний добуток (
) 
0 запишемо цю умову в координатному вигляді:
.
Співпадають: тоді 
(у колінеарних векторів відповідні координати пропорційні).
.
, 
тапозначимо через R та rранги цих матриць. Тоді: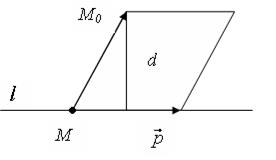
та(l2): 
, то відстань d між ними знаходиться за формулою: 
.
