Варіант 12
1. Скласти рівняння прямої, яка проходить через точку М (2, -5, 3) і паралельна осі Оу. 2. Написати параметричні рівняння прямої 3. Скласти канонічні рівняння прямої 4. Дослідити взаємне розміщення пари прямих: 5. Знайти косинус кута, який утворений прямими: 6. Скласти рівняння прямої, яка проходить через точку М (0, 0, 1) і перетинає кожну з прямих: 7. Скласти рівняння площини, яка проходить через точку М (2, -2, 1) і пряму 8. Знайти точку, симетричну точці А (1, 5, 2) відносно площини 2х – у – z + 11 = 0. 9. Знайти відстань від точки Р (2, 3, -1) до прямої 10. Дано вершини трикутника А(1; -2; -4), В(3; 1; -3) та С(5; 1; -7). Скласти параметричні рівняння його висоти, що опущена з вершини В на протилежну сторону.
Варіант 13 1. Визначити, при якому значенні D пряма 2. Знайти точку перетину площини 5х – 3у + 2z – 30 = 0 з віссю Оу. 3. Пряма задана як лінія перетину площин 2х + 3у – 16z – 7 = 0, 3х + у – 17z = 0. Скласти канонічні рівняння цієї прямої. 4. Дослідити взаємне розміщення пари прямих: 5. Знайти синус кута, утвореного прямою 6. Скласти рівняння прямої, яка проходить через точку М (-1, 2, -3) перпендикулярно до вектора 7. Скласти рівняння площини, яка проходить через дві паралельні прямі 8. Знайти проекцію прямої 9. Знайти відстань від точки Р (2, 3, -1) до прямої Дано трикутник звершинами А(1, 4, -5), В(-3, 6, 9), С(5, 6, 7). Скласти рівняння прямої, на якій лежить медіана, що проведена з вершини В.
|



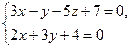 і
і 
 і
і 
 і
і 


 перетинає вісь Оу.
перетинає вісь Оу.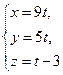 і
і 
 з площиною 3х + у – 2 = 0.
з площиною 3х + у – 2 = 0. = (6, -2, -3) і перетинає пряму
= (6, -2, -3) і перетинає пряму  .
. і
і  .
. на площину ХОY.
на площину ХОY.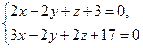 .
.


