Теорема Жуковского
Теорема Жуковского определяет аэродинамическую силу реакции потока на профиль через циркуляцию вокруг профиля. Взаимодействие потока с профилем вызывает появление аэродинамической силы Р, действующей со стороны потока на профиль, равная ей сила и направленная противоположно – сила реакции профиля Р ′ (рис. 4.13) [6].
Рис. 4.13. Схема к выводу теоремы Жуковского
Для определения аэродинамической силы, действующей на профиль, можно воспользоваться результатами теории решеток профилей, основы которой положены Н.Е. Жуковским и С.А. Чаплыгиным. При этом достаточно знать значения средних по шагу скоростей до и после решетки. Проведем вокруг выбранного профиля замкнутый контур (рис. 4.13) так, чтобы расстояние между сторонами bc и ad было равно шагу решетки t и грани dc и ab вынесены настолько далеко от профиля, что скорость и давление не изменяются по шагу решетки ( Определим циркуляцию вокруг контура abcda:
т.к. ab = dc = t, то
Воспользуемся теоремой об изменении количества движения, согласно которой производная по времени от количества движения равна сумме всех сил, действующих на газ:
Рассмотрим элемент газа, массой m, соответствующий отрезку ab и перемещающийся за время dτ; в положение cd. Проинтегрируем уравнение (4.5) Проекция на ось u:
массовый расход газа можно представить как
где тогда
Проекция на ось z:
Перепад давлений (P 1- P 2) определим из уравнения Бернулли
т.к. тогда
Согласно 3-му закону Ньютона (рис. 4.13)
Подставив (4.6) и (4.7) в (4.8), получим
Введем понятие вектора средней скорости (рис. 4.14)
Считая как было принято ранее
Уравнение (4.9) является математическим выражением теоремы Жуковского, согласно которой полная аэродинамическая сила действующая со стороны потока на профиль (подъемная сила) равна произведению плотности газа на среднюю скорость и циркуляцию вокруг профиля. Направление аэродинамической силы Р определяется поворотом вектора Определим влияние вязкости газа на величину аэродинамической силы. Обозначим: Р – подъемная сила в случае идеального газа; R – подъемная сила с учетом вязкости (рис. 4.15).
Проекции подъемной силы на ось u как в случае идеального газа, так и в случае вязкого – одинаковы
Проекции подъемной силы на ось z будут различными для идеального и вязкого газа
где hw – потери энергии на трение, Дж/кг. Из (4.11) перепад давлений
Используя для определения Rz уравнение (4.7), подставим в него перепад давлений из (4.12), получим
где Величины Pz и Rz отрицательные (Pz <0 и Rz <0), т.к. направлены против оси z (рис. 4.15). Отсюда следует, что
Таким образом, в случае обтекания профиля вязким газом в уравнение Бернулли добавляются потери на трение. Это приводит к уменьшению разности давлений (P 1- P 2) и снижению силы Rz по сравнению с силой Pz. Физически это обусловлено наличием силы лобового сопротивления Rw (рис. 4.15). Практическое приложение изложенных в данном разделе 4.6 теоретических основ газовой динамики к компрессорным машинам динамического действия заключается в том, что зная величину подъемной силы, можно определить подводимую к рабочему колесу мощность. Известно, что мощность на валу связана с крутящим моментом. Тогда для каждой точки вдоль радиуса лопатки r справедливо равенство (рис. 4.16)
Для рабочего колеса в целом следует взять интеграл
т.к.
Далее, считая что
Рис. 4.16. К определению мощности подводимой к рабочему колесу:
Таким образом, для определения затрат работы на сжатие газа в ступени компрессора можно воспользоваться теоремой Жуковского, если возможно рассчитать циркуляцию вокруг профиля по реальному распределению скоростей, что является достаточно сложной задачей, решение которой в настоящее время возможно лишь при ряде упрощающих допущений.
|

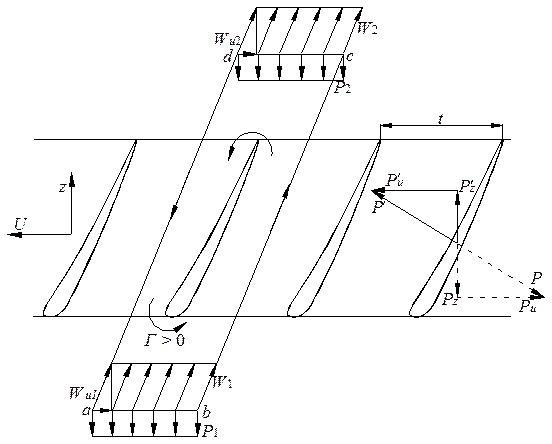
 ;
; 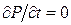 ).
).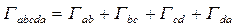 ,
, , тогда
, тогда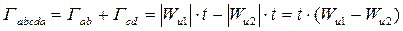 .
. . (4.5)
. (4.5)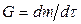 .
.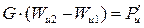 ,
,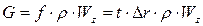 ,
,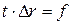 – площадь сечения; ∆ r = 1 – высота сечения,
– площадь сечения; ∆ r = 1 – высота сечения,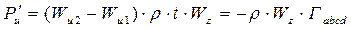 . (4.6)
. (4.6)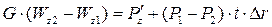 .
. ,
, ,
,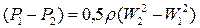 ,
, и
и  , то
, то 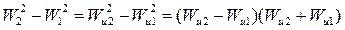 ,
,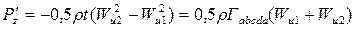 . (4.7)
. (4.7)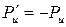 и
и 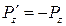 , тогда полная аэродинамическая сила
, тогда полная аэродинамическая сила . (4.8)
. (4.8)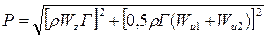 ,
,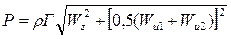 .
. ,
,  ,
,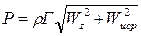 .
.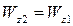 , введя
, введя 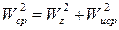 , получим
, получим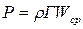 . (4.9)
. (4.9) на 90º против направления циркуляции (Г >0).
на 90º против направления циркуляции (Г >0).
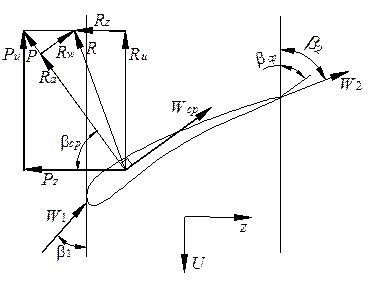
 . (4.10)
. (4.10)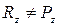 , т.к. уравнение Бернулли для вязкого газа включает потери на трение:
, т.к. уравнение Бернулли для вязкого газа включает потери на трение: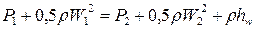 , (4.11)
, (4.11)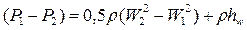 . (4.12)
. (4.12) , (4.13)
, (4.13) .
. , а т.к.
, а т.к. 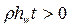 , то по абсолютной величине
, то по абсолютной величине .
.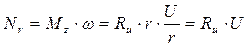 .
.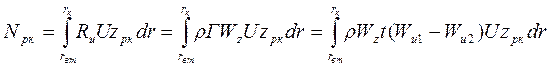 ,
, (рис. 4.16 б) и
(рис. 4.16 б) и  , тогда
, тогда ,
,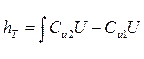 и
и 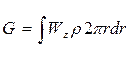 , получим
, получим . (4.14)
. (4.14)



