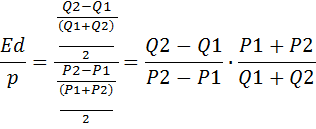Эластичность спроса по цене

Слово «эластичность» происходит от греч. elastikos - эластичный, т.е. упругий, растяжимый, лишенный резкости.

Эластичность спроса - это мера чувствительности величины спроса на товар к изменению какого-либо из факторов, определяющих величину спроса. Согласно закону спроса, в первую очередь рассматривается цена, как главный фактор спроса.

Эластичность спроса по цене (ЭСЦ) определяется на основании обратной функции спроса: Qd = f(P). Именно производная от этой функции показывает, как изменяется зависимая переменная Qd вследствие изменения аргумента P. Производная определяется как предел отношения абсолютных приращений переменных: dQ/dP. Графически этому пределу соответствует угол наклона касательной к кривой спроса.

Однако в экономике показатель производной функции неудобен, так как зависит от выбора единиц измерения. Например, производная будет измеряться в кг/руб., т/руб. и т.д. Поэтому для сравнительного анализа эластичности спроса на различные товары используется связь (отношение) не абсолютных изменений величин Р и Q, а их процентных изменений.

Соотношение процентных изменений величин Р и Q измеряется только числом (цифрой), которое называется коэффициентом эластичности спроса по цене, обозначается Ed/p и рассчитывается по формуле:

 

Ed/p =	процентное изменение объема спроса
процентное изменение цены товара

Существует два метода расчета коэффициента Ed/p - точечная эластичность и дуговая эластичность. Считается, что наиболее точные значения Ed/p получаются при расчете точечной эластичности, которая соответствует углу наклона касательной к одной точке кривой спроса. Однако этот метод предполагает знание функции спроса на товар в данный конкретный период времени, что в большинстве случаев крайне затруднительно.

Дуговая эластичность - это мера чувствительности величины спроса, отражающая конечное изменение цен, которое характеризуется перемещением от одной точки кривой спроса к другой. Обычно в практике используется дуговая эластичность, расчет которой не предполагает вывода функции спроса.

Для иллюстрации техники вычисления дуговой эластичности, рассмотрим кривую спроса, на которой имеются две точки А и Б со следующими комбинациями цены и объема:

 

Точки	Цена, рублей	Величина спроса, шт.
А
Б

 

Здесь возможно получить три значения коэффициента Ed/p

1. При снижении цены товара с 12 руб. до 10 руб. этот коэффициент равен:

 

Ed/p =	(30-50)/50	= - 2,0
(12-10)/10

 

2. При увеличении цены с 10 руб. до 12 руб. коэффициент Ed/p равен:

Ed/p =	(30-50)/50	= - 4,0
(10-12)/12

 

3. Однако практически рассчитывается одна, средневзвешенная величина коэффициента Ed/p, согласно формуле:

 

Если в данную формулу подставить вышеназванные значения цены и объема, то получится следующий результат:

Известно, что в большинстве случаев с повышением цены товара величина спроса на него снижается. Поэтому можно сказать, что эластичность спроса по цене всегда отрицательна. При анализе спроса знак эластичности не представляет интереса. Как следствие, для измерения величины реакции (чувствительности) спроса на изменение цены удобнее использовать лишь абсолютную величину коэффициента эластичности, т.е. Ed/p.

В зависимости от принимаемых значений коэффициента Ed/p спрос бывает:

- эластичным, если Ed/p> 1;

- неэластичным, если Ed/p< 1;

- единичной эластичности, если Ed/p = 1;

- совершенно эластичным, если Ed/p = ∞

- совершенно неэластичным, если Ed/p = 0.

Все эти виды эластичности спроса по цене можно проиллюстрировать с помощью наклона кривой спроса в диапазоне от горизонтальной линии (совершенно эластичный спрос) до вертикальной линии (совершенно неэластичный спрос).