Неинерциальные системы отсчета. Силы инерции в системах, движущихся поступательно и во вращающихся системах отсчета.
Законы Ньютона выполняются только в инерциальных системах отсчета Системы отсчета, движущиеся с ускорением относительно инерциальных, называют неинерциальными. В этих системах законы динамики можно применять, если кроме сил, обусловленных воздействием тел друг на друга, ввести рассмотрение сил особого рода – так называемых сил инерции. Проявление этих сил необходимо учитывать: 1) при ускоренном поступательном движении системы отсчета; 2) при рассмотрении тел, покоящихся во вращающейся системе отсчета; 3) при рассмотрении тел, движущихся во вращающейся системе отсчета.
I. Пусть на горизонтальном прямолинейном участке железнодорожного пути находится платформа, а на полу вагона шар. Трения между шаром и платформой нет. Когда вагон покоится, шар неподвижен в обеих системах отсчета. Оба наблюдателя видят одно и то же. Уравнение движения: Если вагон движется с ускорением Для наблюдателя в системе К’ шар движется с ускорением По второму закону Ньютона наблюдатель в системе К’ скажет, что на шар массой m действует сила Уравнение Таким образом, на все тела, находящиеся в поступательно движущихся системах отсчета кроме обычных сил действуют силы инерции, равные произведению массы тела и ускорения системы, взятому с обратным знаком. Уравнение движения в неинерциальных системах отсчета имеют такой же вид, как в инерциальных системах отсчета, только в сумму действующих на него сил входят наряду с ньютоновскими и силы инерции:
II. Пусть диск равномерно вращается с угловой скоростью w (w=const) вокруг вертикальной оси, проходящей через его центр. На диске установлен пружинный маятник, представляющий собой шарик на спице, прикрепленный к пружине. При вращении диска пружина растягивается. Для наблюдателя в системе К шар движется по окружности радиусом R. Следовательно на него действует сила, равная Для наблюдателя в системе К’ шар покоится. Это возможно, если сила упругости уравновешивается равной и противоположно направленной ей силой
III. Пусть шарик массой m движется с постоянной скоростью v вдоль радиуса равномерно вращающегося диска (v=const, w=const, v^w). Если диск не вращается, то шарик, направленный вдоль радиуса, попадает в точку А, если же диск привести во вращение в направлении, указанном стрелкой, то шарик покатися по кривой ОВ (см. рис.), причем его скорость относительно диска изменяет свое направление. Это возможно, если на шарик действует сила, перпендикулярная скорости v. Эта сила называется кориолисовой силой инерции. Она равна:
Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчета, например, относительно Земли. Поэтому действием этих сил объясняется ряд наблюдаемых на Земле явлений. Так, если тело движется в северном полушарии на север, то действующая на него сила Кориолиса будет направлена вправо по отношению к направлению движения, то есть тело несколько отклонится на восток. Если тело движется на юг, о сила Кориолиса также действует вправо, если смотреть по направлению движения, то есть тело отклонится на запад. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек, правые рельсы по движению изнашиваются быстрее и т.д. Итак, во вращающихся системах отсчета на все движущиеся тела действуют две силы инерции – центробежная сила и сила Кориолиса. Обобщим полученный результат для всех неинерциальных систем отсчета и получим основной закон динамики для неинерциальных систем отсчета: Силы инерции действуют только в неинерциальных системах отсчета. В инерциальных системах отсчета таких сил не существует.
|


 . Все происходит в соответствии с законом Ньютона, то есть обе системы отсчета являются инерциальными.
. Все происходит в соответствии с законом Ньютона, то есть обе системы отсчета являются инерциальными. , то наблюдатели в разных системах отсчета видят разные явления. Для наблюдателя, находящегося в системе К: шар покоится:
, то наблюдатели в разных системах отсчета видят разные явления. Для наблюдателя, находящегося в системе К: шар покоится: 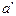 , направленным против ускорения вагона, причем
, направленным против ускорения вагона, причем 
 , но нет тела, вызывающего действие этой силы, хотя
, но нет тела, вызывающего действие этой силы, хотя  . То есть, в неинерциальных системах отсчета не «работают» законы Ньютона. Введем силу инерции, которая вызвана не взаимодействием тел. а является результатом ускоренного движения системы отсчета
. То есть, в неинерциальных системах отсчета не «работают» законы Ньютона. Введем силу инерции, которая вызвана не взаимодействием тел. а является результатом ускоренного движения системы отсчета  .Для наблюдателя в системе К’ второй закон Ньютона:
.Для наблюдателя в системе К’ второй закон Ньютона:  .
.
 .
.
 и направленная вдоль по спице перпендикулярно к оси вращению диска:. Она равна силе упругости, возникшей в пружине, направленной к центру диска. Поэтому сила упругости и создает нормальное ускорение, то есть
и направленная вдоль по спице перпендикулярно к оси вращению диска:. Она равна силе упругости, возникшей в пружине, направленной к центру диска. Поэтому сила упругости и создает нормальное ускорение, то есть  . Явление происходит в соответствии со вторым законом Ньютона.
. Явление происходит в соответствии со вторым законом Ньютона. :
:  . Сила
. Сила  .
.
 . Вектор
. Вектор  перпендикулярен векторам скорости тела и угловой скорости вращения системы отсчета в соответствии с правилом правого винта.
перпендикулярен векторам скорости тела и угловой скорости вращения системы отсчета в соответствии с правилом правого винта.
 .
.


