Механический принцип относительности.
Динамика – раздел механики, в котором изучается механическое движение с учетом причин, вызывающих движение. Основные понятия динамики – масса и сила. Масса – физическая величина, характеризующая инертность тел. Инертность – это свойство тел сохранять состояние покоя или равномерного прямолинейного движения. Проявляется в том, что тело нельзя мгновенно остановить или вывести из состояния покоя. За единицу массы принят эталон–сплав платины и иридия, хранящийся в палате мер и весов в Париже. m – величина скалярная, [ m ]=кг. Сила – физическая величина, характеризующая действие одного тела на другое, в результате чего у тела изменяется скорость, то есть появляется ускорение, или происходит деформация тела, либо имеет место и то, и другое. Действие силы зависит не только от ее величины, но и от направления, то есть сила Первый закон Ньютона гласит: существуют такие системы отсчета, относительно которых тело покоится или движется прямолинейно и равномерно, если на него не действуют другие тела или действие этих тел компенсировано. Такие системы отсчета называются инерциальными. Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил. Он гласит: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела):
Соотношению (1) можно придать другой вид, представив его в виде:
В классической механике масса тела есть величина постоянная (не зависящая от скорости), внесем ее под знак производной:
Векторная величина
Это выражение – более общая формулировка второго закона Ньютона: скорость изменения импульса материальной точки равно действующей на нее силе. Выражение (4) называется уравнением движения материальной точки. Из второго закона также получим размерность силы: Третий закон Ньютона определяет взаимодействие между материальными точками (телами): всякое действие материальных точек (тел) друг на друга носит характер взаимодействия. Количественно это описывается третьим законом Ньютона: две материальные точки действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны вдоль соединяющей эти точки прямой:
где Законы Ньютона в классической механике применимы для описания движения: а) макротел; б) для тел постоянной массы; в) при скоростях, значительно меньших скорости света. В механике Ньютона все законы выполняются в инерциальных системах отсчета. Пусть имеем две инерциальные системы отсчета, одну из которых мы будем условно считать неподвижной (система К с осями декартовых координат х,у,z). Другая же система (система К’ с осями декартовых координат х ’, у ’, z ’) пусть равномерно и прямолинейно движется со скоростью
Преобразования Галилея связывают координаты и время события в указанных двух инерциальных системах отсчета.
Преобразования Галилея в векторной форме:
Продифференцируем по времени и учтем, что
В классической механике считается, что масса тела не зависит от системы отсчета, то есть
Таким образом, закон Ньютона не изменяется при переходе от системы К в систему К’. На этом основании сформулируем механический принцип относительности Галилея: во всех инерциальных системах отсчета одни и те же механические явления протекают одинаковым образом, и никакими механическими опытами, проводимыми внутри данной инерциальной системы отсчета, невозможно установить, покоится система отсчета или движется равномерно и прямолинейно. Механический принцип относительности свидетельствует о том, что в механике все инерциальные системы отсчета совершенно равноправны. На основе законов механики нельзя выделить из множества инерциальных систем отсчета какую-то «главную» ИСО, которая бы обладала какими-либо преимуществами перед другими, так что движение тел относительно нее можно бы рассматривать как их «абсолютное движение», а покой – как «абсолютный покой». 3. Законы сохранения в нерелятивистской механике. Рассмотрим механическую систему, состоящую из n материальных точек. Все тела, не входящие в рассматриваемую механическую систему, называются внешними, а силы, действующие со стороны этих тел, называются внешними силами. Силы взаимодействия частей самой системы называются внутренними. Пусть Рассмотрим замкнутую изолированную систему. Механическая система, на которую не действуют внешние силы, называют замкнутой системой. Тогда Из (1) следует, что Мы пришли к закону сохранения полного импульса изолированной системы: при любом характере взаимодействия тел, образующих замкнутую систему, вектор полного импульса этой системы все время остается постоянным. Закон сохранения полного импульса изолированной системы – это универсальный закон природы. В более общем случае, когда система незамкнута, то полный импульс незамкнутой системы не остается постоянным. Его изменение за единицу времени равно геометрической сумме всех внешних сил. Энергия –это единая количественная мера различных форм движения материи и соответствующих форм взаимодействий. В механике различают кинетическую и потенциальную энергию. Кинетической энергией называют энергию движущегося тела. Она зависит от скорости движения тела и ею обладают все движущиеся тела. Ее величина определяется формулой Потенциальная энергия – это энергия взаимодействия тел или частей одного и того же тела. Потенциальная энергия тела в поле силы тяжести Полная механическая энергия системы Консервативной называется система, в которой работа сил при перемещении по замкнутому контуру равна нулю. Если консервативная система замкнута, то внешние силы отсутствуют:
закон сохранения замкнутой консервативной системы: Сумма кинетической и потенциальной энергии всех материальных точек, входящих в замкнутую консервативную систему, остается величиной постоянной, какие бы изменения не происходили. Если система подвергается действию неконсервативных (диссипативных) сил, механическая энергия убывает, переходя в другие виды энергии (например, тепловую при действии сил трения). Но в целом энергия остается постоянной. Тогда в соответствии со всеобщим законом сохранения и превращения энергии – энергия никуда не исчезает и не появляется вновь, а лишь переходит от одного тела к другому или превращается из одного вида в другой. Если материальная точка массой mi движется по окружности ради у са ri вокруг неподвижного центра под действием силы Уравнение движения такого тела называют основным законом динамики вращательного движения и оно имеет вид
где
|

 – векторная величина, [
– векторная величина, [  , где К – коэффициент пропорциональности. В системе СИ К=1. Тогда:
, где К – коэффициент пропорциональности. В системе СИ К=1. Тогда:
 . (2)
. (2) . (3)
. (3) , численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом этой материальной точки. Подставляя это выражение в (3), получим:
, численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом этой материальной точки. Подставляя это выражение в (3), получим: . (4)
. (4) .
. ,
, – сила, действующая на первую материальную точку со стороны второй;
– сила, действующая на первую материальную точку со стороны второй;  – сила, действующая на вторую материальную точку со стороны первой.
– сила, действующая на вторую материальную точку со стороны первой.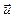 относительно первой (см. рис.2.1)
относительно первой (см. рис.2.1)
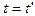 (1)
(1)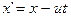 (2)
(2) (3)
(3) (4)
(4) . Дифференцируя эту формулу по времени, получим классический закон сложения скоростей:
. Дифференцируя эту формулу по времени, получим классический закон сложения скоростей:
 . Получим:
. Получим: (8)
(8)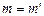 . Умножим обе части равенства (8) на m:
. Умножим обе части равенства (8) на m: или
или 
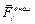 – сумма всех внешних сил, действующих на i-ю точку системы,
– сумма всех внешних сил, действующих на i-ю точку системы,  – импульс механической системы. Используя законы Ньютона, можно получить закон изменения импульса механической системы:
– импульс механической системы. Используя законы Ньютона, можно получить закон изменения импульса механической системы:  –производная по времени от импульса механической системы равна вектору внешних сил, действующих на систему.
–производная по времени от импульса механической системы равна вектору внешних сил, действующих на систему. =0. Из закона динамики для системы тел (материальных точек):
=0. Из закона динамики для системы тел (материальных точек):  (1)
(1) или
или  (2)
(2) , где С – произвольная постоянная. В классической механике обычно считают С=0.
, где С – произвольная постоянная. В классической механике обычно считают С=0. =
=  , потенциальная энергия упруго деформированного тела –
, потенциальная энергия упруго деформированного тела – 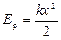 .
. . Для системы материальных точек
. Для системы материальных точек  – изменение полной механической энергии в незамкнутой консервативной системе равна работе внешних сил.
– изменение полной механической энергии в незамкнутой консервативной системе равна работе внешних сил. Þ
Þ  Þ
Þ 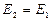 E = const.
E = const.
 – момент инерции материальной точки относительно точки О, а моментом силы относительно заданной оси вращения называют величину
– момент инерции материальной точки относительно точки О, а моментом силы относительно заданной оси вращения называют величину 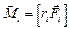 . Величина
. Величина  –плечо силы, тогда модуль момента силы:
–плечо силы, тогда модуль момента силы:  определяется как произведение силы на плечо. Любое твердое тело рассматривается как система материальных точек и момент инерции твердого тела определяется как
определяется как произведение силы на плечо. Любое твердое тело рассматривается как система материальных точек и момент инерции твердого тела определяется как 
 , где
, где  –вектор углового ускорения:
–вектор углового ускорения: 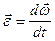 . В дифференциальной форме этот закон:
. В дифференциальной форме этот закон:  . Введем понятие момента импульса, которое определяется формулой
. Введем понятие момента импульса, которое определяется формулой  . Тогда
. Тогда  . В замкнутой системе момент внешних сил
. В замкнутой системе момент внешних сил  и Þ
и Þ  , откуда:
, откуда: ,
, – векторная сумма моментов тел, входящих в эту систему. Данное выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, то есть не изменяется с течением времени.
– векторная сумма моментов тел, входящих в эту систему. Данное выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, то есть не изменяется с течением времени.


