МКТ. Основное уравнение кинетической теории газов. Газовые законы. Уравнение Менделеева-Клапейрона.
Основным уравнением кинетической теории газов называется соотношение, связывающее давление (величину, измеряемую на опыте) со скоростью или кинетической энергией молекулы идеального газа. В молекулярно-кинетической теории пользуются идеализированной моделью идеального газа, согласно которой считают, что: 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; 2) между молекулами газа отсутствуют силы взаимодействия; 3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие. Скорости частиц как по модулю, так и по направлению могут быть любыми, изменение их происходит непрерывно.
Рассмотрим одноатомный идеальный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами очень мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда элементарную площадку Ds (cм. рис.). При каждом соударении, молекула, движущаяся перпендикулярно площадке, передает ей импульс т0 v –(–m0 v ) = 2 т0 v, где т0 — масса молекулы, v – ее скорость. За время D t площадки Ds достигнут только те молекулы, которые заключены в объеме цилиндра с основанием Ds и высотой vD t. Число этих молекул равно n DsvD t, где п – концентрация молекул. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина из них (1/6) движется вдоль данного направления в одну сторону, половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку Ds будет Тогда давление газа на стенку сосуда: Если газ в объеме V содержит N молекул, движущихся со скоростями v1, v2., то учитывают среднюю квадратичную скорость: Данное выражение называется основным уравнением молекулярно-кинетической теории идеальных газов. Оно устанавливает связь между давлением и среднеквадратичной скоростью. Введем Е Здесь давление связано со средней энергией поступательного движения молекул. При переходе к равновесию от одной части газа к другой передается энергия. Выравнивается не энергия всего газа как целого, а средняя кинетическая энергия, отнесенная к одной молекуле. Температура газа пропорциональна средней кинетической энергии его молекул: Т ~ Е. Средняя кинетическая энергия поступательного движения молекулы Е = где k - постоянная Больцмана,: k =1,38.10-23 Дж/К, Т – температура, выраженная в кельвинах. Из формулы (4) следует, что абсолютная температура является мерой средней кинетической энергии поступательного хаотического движения молекул. Подставляя в (3) это выражение, получим, что давление идеального газа связано с температурой соотношением:
Давление определяется только концентрацией (при постоянной температуре) и не зависит от сорта молекул. Газовые законы устанавливают связь между двумя параметрами состояния при постоянном третьем параметре для данной массы газа.
Экспериментальное исследование свойств газов, проведенное в ХVII-XVIII вв. Бойлем, Мариоттом, Гей-Люссаком, Шарлем, привело к формулировке газовых законов (с учетом представления абсолютной температуры) 1. Изотермический процесс. pV =const – уравнение изотермы. Чем выше изотерма, тем более высокой температуре она соответствует, T2>T1. 2. Изобарный процесс.
3. Изохорический процесс. Комбинируя выражения газовых законов, получим уравнение, связывающее р, V, Т (объединенный газовый закон): Постоянная в этом уравнении определяется экспериментально. Для количества вещества 1 моль газа она оказалась равной R=8,31 1 моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг. Число молекул (структурных единиц) в 1 моле равно числу Авогадро: NA=6,02.1023моль-1. Для R справедливо соотношение: R = k NA. Итак, для одного моля: уравнение Менделеева-Клапейрона.
|

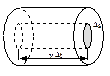
 . При столкновении с площадкой эти молекулы передадут ей импульс:
. При столкновении с площадкой эти молекулы передадут ей импульс: 
 .
. (1)
(1)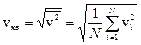 (2), характеризующую всю совокупность молекул газа. Уравнение (1) с учетом (2) примет вид
(2), характеризующую всю совокупность молекул газа. Уравнение (1) с учетом (2) примет вид  . (3)
. (3) – среднюю кинетическую энергию хаотического поступательного движения одной молекулы, тогда основное уравнение запишется как:
– среднюю кинетическую энергию хаотического поступательного движения одной молекулы, тогда основное уравнение запишется как:  или
или  Е.
Е. , (4)
, (4) .
.
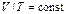 – уравнение изобары. Чем ниже к оси температуры наклонена изобара, тем большему давлению она соответствует, р2 > p1.
– уравнение изобары. Чем ниже к оси температуры наклонена изобара, тем большему давлению она соответствует, р2 > p1.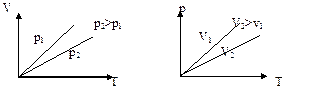
 – уравнение изохоры. График зависимости р от Т изображен на рис 7.3. Чем ниже к оси температуры наклонена изохора, тем большему объему она соответствует, V 2 > V 1.
– уравнение изохоры. График зависимости р от Т изображен на рис 7.3. Чем ниже к оси температуры наклонена изохора, тем большему объему она соответствует, V 2 > V 1. .
. и была названа универсальной газовой постоянной.
и была названа универсальной газовой постоянной. . Для произвольного количества газа n =m/ m(m - молярная масса газа.):
. Для произвольного количества газа n =m/ m(m - молярная масса газа.):  ,
,


