Закон всемирного тяготения. Гравитационное поле.
В XVII в. Кеплер открыл и сформулировал законы движения планет: 1. Планеты обращаются вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце. 2. Радиус-вектор, проведенный о Солнца к планете за равные промежутки времени описывает одинаковые площади. 3. Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит: На их основе Ньютон установил, что сила притяжения между планетой и Солнцем прямо пропорциональна их массам и обратно пропорциональна квадрату расстояния между планетой и Солнцем: где М – масса Солнца, m –масса планеты, R – расстояние между ними. Ньютон также доказал, что этот вывод справедлив не только для небесных тел, но и для любых двух материальных объектов и сформулировал закон всемирного тяготения: между любыми двумя телами действует сила тяготения, прямо пропорциональная массам тел и обратно пропорциональная квадрату расстояния между ними: где g – гравитационная постоянная, Границы применимости закона всемирного тяготения: а) оба тела материальны точки; б) взаимодействуют два шара любых размеров; в) большое тело имеет форму шара, малое – любую форму.
Гравитационная постоянная численно равна силе тяготения, которая действует между телами единичной массы, находящимися на расстоянии 1 м. Она имеет значение: g=6,67.10-11 Ньютон не указал причину тяготения, но высказал мысль о посреднике действия между телами. В настоящее время по аналогии с электромагнитным полем посредником принято считать гравитационное поле – особая форма материи, окружающее любое тело. Каждая точка поля тяготения характеризуется напряженностью Пусть тело М – источник поля. Тогда в точке, где находится тело m, напряженность поля: Можно показать, что Силы тяготения – это консервативные силы. Можно поэтому ввести в рассмотрение соответствующую потенциальную энергию, которая для тел, находящихся на расстоянии r друг от друга определится как:
Гравитационный потенциал точки поля, в котором находится тело m, равен
Здесь
Графически напряженность и потенциал характеризуются линиями напряженности и эквипотенциальными поверхностями. Касательная к линии напряженности в данной точке совпадает с вектором
|


 .
. ,
, – единичный вектор.
– единичный вектор.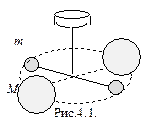
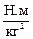 (
( ). Впервые величина g была определена в лаборатории Кавендиша с помощью крутильных весов в 1798 г. (рис.4.1.) Она определялась по углу закручивания проволоки, на которой было закреплено коромысло, а на его концах подвешены пробные шары малой массы. Вблизи них располагались два массивных шара, расположенные на тяжелом фундаменте. Поворотом этого фундамента большие шары приближались к малым, в результате маленькие шары притягивались к большим.
). Впервые величина g была определена в лаборатории Кавендиша с помощью крутильных весов в 1798 г. (рис.4.1.) Она определялась по углу закручивания проволоки, на которой было закреплено коромысло, а на его концах подвешены пробные шары малой массы. Вблизи них располагались два массивных шара, расположенные на тяжелом фундаменте. Поворотом этого фундамента большие шары приближались к малым, в результате маленькие шары притягивались к большим. и потенциалом j.
и потенциалом j. 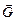 является силовой характеристикой гравитационного поля, а j является энергетической характеристикой поля.
является силовой характеристикой гравитационного поля, а j является энергетической характеристикой поля. . Подставим вместо
. Подставим вместо  его значение, получим:
его значение, получим: 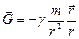 (1).
(1). (2).
(2). . Подставляя вместо Еп его значение, найдем, от каких физических факторов зависит j (в случае точечного источника поля):
. Подставляя вместо Еп его значение, найдем, от каких физических факторов зависит j (в случае точечного источника поля):  (3). Из (1)-(3) вытекает связь между
(3). Из (1)-(3) вытекает связь между  . (4)
. (4) – градиент потенциала, показывает, как изменяется потенциал при изменении r. Знак минус указывает на то, что вектор напряженности направлен в сторону убывания потенциала.
– градиент потенциала, показывает, как изменяется потенциал при изменении r. Знак минус указывает на то, что вектор напряженности направлен в сторону убывания потенциала.



