(метод векторных диаграмм)
Решение ряда задач значительно облегчается и становится наглядным, если изображать колебания графически в виде векторов на плоскости. Изображенная таким способом схема колебаний называется векторной диаграммой.
Рассмотрим произвольный вектор 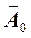 , образующий с осью
, образующий с осью  угол
угол 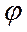 . Если привести этот вектор во вращение относительно точки
. Если привести этот вектор во вращение относительно точки 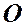 , с угловой скоростью
, с угловой скоростью  , то проекция конца вектора будет перемещаться по оси
, то проекция конца вектора будет перемещаться по оси  (опорной линии) в пределах от
(опорной линии) в пределах от  до
до  . Координата этой проекции будет изменяться со временем по закону:
. Координата этой проекции будет изменяться со временем по закону:
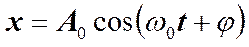
Следовательно, проекция конца вектора  будет совершать гармоническое колебание с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной
будет совершать гармоническое колебание с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной  (углу, образованному вектором
(углу, образованному вектором  в начальный момент времени).
в начальный момент времени).
 Если j > 0, то j – откладывается "вверх" – против часовой стрелки по отношению к опорной линии.
Если j > 0, то j – откладывается "вверх" – против часовой стрелки по отношению к опорной линии.  – проекция вектора
– проекция вектора  на опорную линию.
на опорную линию.
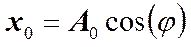 – т.е. проекция вектора
– т.е. проекция вектора  равна смещению
равна смещению  в момент времени t = 0.
в момент времени t = 0.
При w > 0 вращение происходит против часовой стрелки. За промежуток времени t вектор амплитуды  повернётся на угол wt и займёт новое положение. Его проекция на опорную линию будет равна
повернётся на угол wt и займёт новое положение. Его проекция на опорную линию будет равна  . За время равное периоду колебаний T, вектор амплитуды
. За время равное периоду колебаний T, вектор амплитуды  повернётся на угол 2p, и проекция вектора амплитуды совершит полное колебание около положения равновесия (точки О). Следовательно, вращающийся вектор амплитуды полностью характеризует гармоническое колебание.
повернётся на угол 2p, и проекция вектора амплитуды совершит полное колебание около положения равновесия (точки О). Следовательно, вращающийся вектор амплитуды полностью характеризует гармоническое колебание.
Таким образом, гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью  угол, равный начальной фазе колебания.
угол, равный начальной фазе колебания.
Этим представлением широко пользуются.
Сложение гармонических колебаний,

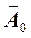 , образующий с осью
, образующий с осью  угол
угол 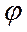 . Если привести этот вектор во вращение относительно точки
. Если привести этот вектор во вращение относительно точки 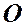 , с угловой скоростью
, с угловой скоростью  , то проекция конца вектора будет перемещаться по оси
, то проекция конца вектора будет перемещаться по оси  до
до  . Координата этой проекции будет изменяться со временем по закону:
. Координата этой проекции будет изменяться со временем по закону: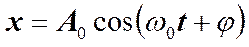
 будет совершать гармоническое колебание с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной
будет совершать гармоническое колебание с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной  (углу, образованному вектором
(углу, образованному вектором  Если j > 0, то j – откладывается "вверх" – против часовой стрелки по отношению к опорной линии.
Если j > 0, то j – откладывается "вверх" – против часовой стрелки по отношению к опорной линии.  – проекция вектора
– проекция вектора  на опорную линию.
на опорную линию.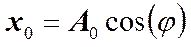 – т.е. проекция вектора
– т.е. проекция вектора  . За время равное периоду колебаний T, вектор амплитуды
. За время равное периоду колебаний T, вектор амплитуды  угол, равный начальной фазе колебания.
угол, равный начальной фазе колебания.


