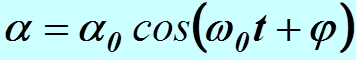Математический маятник – это идеализированная система, состоящая из материальной точки массой 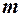 , подвешенной на невесомой нерастяжимой нити, и совершающая колебания под действием силы тяжести.
, подвешенной на невесомой нерастяжимой нити, и совершающая колебания под действием силы тяжести.
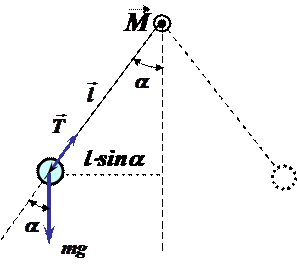 Изобразим такой маятник в момент, когда нить подвеса отклонена влево от вертикали на угол
Изобразим такой маятник в момент, когда нить подвеса отклонена влево от вертикали на угол 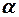 , маятник движется влево. Введем следующие обозначения:
, маятник движется влево. Введем следующие обозначения: 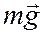 – сила тяжести,
– сила тяжести, 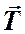 – сила натяжения нити,
– сила натяжения нити, 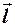 – радиус-вектор.
– радиус-вектор.
Момента силы тяжести 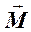 относительно оси. Вектор угловой скорости
относительно оси. Вектор угловой скорости 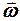 направлен вдоль оси вращения так, что образует правый винт с направлением вращения (движения) маятника. Угловое ускорение
направлен вдоль оси вращения так, что образует правый винт с направлением вращения (движения) маятника. Угловое ускорение 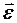 совпадает по направлению с вектором
совпадает по направлению с вектором 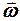 , если угловая скорость увеличивается, и направлено в противоположную сторону, если скорость уменьшается. Пренебрежем силами трения и сопротивления среды. Для получения уравнения движения применим основной закон вращательного движения твердого тела.
, если угловая скорость увеличивается, и направлено в противоположную сторону, если скорость уменьшается. Пренебрежем силами трения и сопротивления среды. Для получения уравнения движения применим основной закон вращательного движения твердого тела.
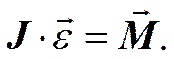
В этом уравнении 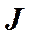 – момент инерции точки относительно оси, проходящей через точку подвеса. Момент силы тяжести
– момент инерции точки относительно оси, проходящей через точку подвеса. Момент силы тяжести 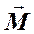 стремится возвратить маятник в положение равновесия; момент силы натяжения нити относительно той же оси равен нулю.
стремится возвратить маятник в положение равновесия; момент силы натяжения нити относительно той же оси равен нулю.
Величины, входящие в уравнение запишем следующим образом:
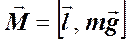 ,
, 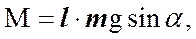
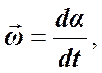
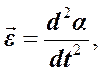 ,
, 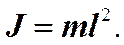
Отсюда основной закон вращательного движения в проекции на ось вращения может быть записан в следующем виде.
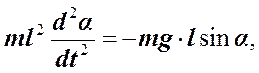
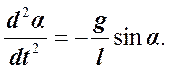
Знак "минус" означает, что действие силы тяжести направлено против движения маятника. Окончательно получим.
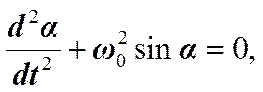
где 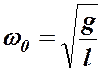
В итоге получили обыкновенное нелинейное дифференциальное уравнение, описывающее движение математического маятника при любой величине угла отклонения от вертикали. Если рассматривать малые отклонения маятника от положения равновесия 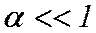 , то из выражения следует дифференциальное уравнение гармонических колебаний (при
, то из выражения следует дифференциальное уравнение гармонических колебаний (при 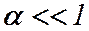
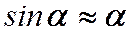 ):
):
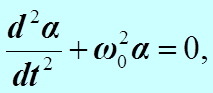
при этом 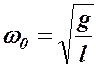 имеет смысл собственной круговой частоты малых колебаний математического маятника. Период этих колебаний определяется по формуле
имеет смысл собственной круговой частоты малых колебаний математического маятника. Период этих колебаний определяется по формуле 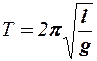 . Решением этого уравнения является известная формула гармонических колебаний
. Решением этого уравнения является известная формула гармонических колебаний
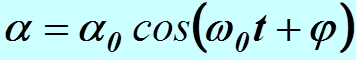

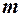 , подвешенной на невесомой нерастяжимой нити, и совершающая колебания под действием силы тяжести.
, подвешенной на невесомой нерастяжимой нити, и совершающая колебания под действием силы тяжести. Изобразим такой маятник в момент, когда нить подвеса отклонена влево от вертикали на угол
Изобразим такой маятник в момент, когда нить подвеса отклонена влево от вертикали на угол 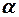 , маятник движется влево. Введем следующие обозначения:
, маятник движется влево. Введем следующие обозначения: 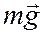 – сила тяжести,
– сила тяжести, 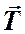 – сила натяжения нити,
– сила натяжения нити, 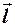 – радиус-вектор.
– радиус-вектор.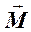 относительно оси. Вектор угловой скорости
относительно оси. Вектор угловой скорости 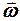 направлен вдоль оси вращения так, что образует правый винт с направлением вращения (движения) маятника. Угловое ускорение
направлен вдоль оси вращения так, что образует правый винт с направлением вращения (движения) маятника. Угловое ускорение 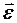 совпадает по направлению с вектором
совпадает по направлению с вектором 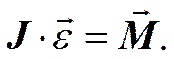
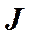 – момент инерции точки относительно оси, проходящей через точку подвеса. Момент силы тяжести
– момент инерции точки относительно оси, проходящей через точку подвеса. Момент силы тяжести 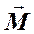 стремится возвратить маятник в положение равновесия; момент силы натяжения нити относительно той же оси равен нулю.
стремится возвратить маятник в положение равновесия; момент силы натяжения нити относительно той же оси равен нулю.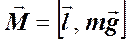 ,
, 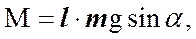
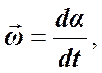
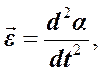 ,
, 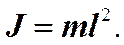
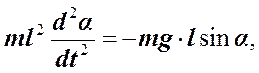
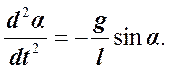
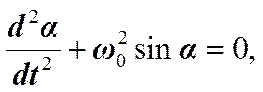
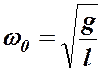
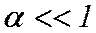 , то из выражения следует дифференциальное уравнение гармонических колебаний (при
, то из выражения следует дифференциальное уравнение гармонических колебаний (при 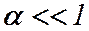
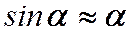 ):
):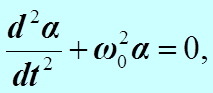
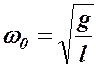 имеет смысл собственной круговой частоты малых колебаний математического маятника. Период этих колебаний определяется по формуле
имеет смысл собственной круговой частоты малых колебаний математического маятника. Период этих колебаний определяется по формуле 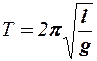 . Решением этого уравнения является известная формула гармонических колебаний
. Решением этого уравнения является известная формула гармонических колебаний