Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.
Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях вдоль осей
Для нахождения уравнения траектории результирующего колебания исключим из уравнений параметр
Преобразуем второе уравнение и распишем его через косинус суммы.
Перепишем последнее уравнение следующим образом и возведём левую и правую части в квадрат.
Перепишем.
Преобразуем.
И окончательно запишем.
Или в общем виде.
Это есть уравнение эллипса, оси которого ориентированы произвольно относительно осей x и y. Исследуем уравнение (1) и выясним форму кривых, определяемых этим уравнением. а) Пусть разность фаз
При четных
При нечетных
Следовательно, в результате сложения двух взаимно перпендикулярных колебаний с одинаковыми начальными фазами и частотами колебания будут происходить вдоль прямой, проходящей через начало координат.
б) Пусть разность фаз будет любой, кроме уже рассмотренных значений. Тогда уравнением траектории будет выражение (1). Это уравнение эллипса. Таким образом, точка, участвующая в двух взаимно перпендикулярных колебаниях с одинаковой частотой, движется по эллиптической траектории, соответствующим образом ориентированной по отношению к выбранной системе координат. Параметры траектории определяются соотношением амплитуд и разностью фаз исходных колебаний. Пример: если
Это так называемое каноническое уравнение эллипса с полуосями A и B. На рисунке стрелками показано направление движения точки вдоль траектории при При Все остальные разности фаз дают эллипсы с различным углом наклона относительно осей координат. Если частоты взаимно перпендикулярных колебаний неодинаковы, то траектория результирующего движения может иметь вид сложных кривых, называемых фигурами Лиссажу. Пример: Пусть отношение частот взаимно перпендикулярных колебаний равно 1:2 и разность фаз
Результирующее колебание показано на рисунке. Траектория вырождается в незамкнутую кривую, по которой точка движется туда и обратно. Это одна из простейших фигур Лиссажу. Возможно, на лабораторном практикуме Вы будете выполнять эту лабораторную работу.
|

 и
и  . Такой случай возникает, например, если на управляющие вертикальные и горизонтальные пластины осциллографа подать периодические гармонические сигналы. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю (Dj = j2 – j1 = j). Тогда уравнения колебаний будут иметь вид:
. Такой случай возникает, например, если на управляющие вертикальные и горизонтальные пластины осциллографа подать периодические гармонические сигналы. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю (Dj = j2 – j1 = j). Тогда уравнения колебаний будут иметь вид:
 ;
; ;
; :
: ;
; 




 (1)
(1)
 ,
,  Из (1) при этом следует
Из (1) при этом следует
 получается
получается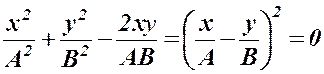 , или
, или 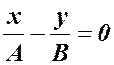 ,
, 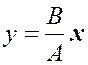
 получается
получается  .
.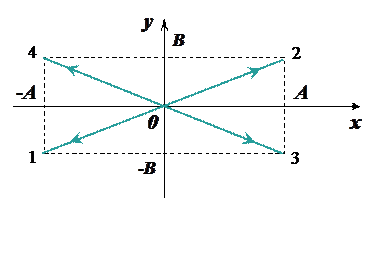 Первому из полученных уравнений соответствует прямая 1 – 2 на рисунке, второму уравнению – прямая 3 – 4.
Первому из полученных уравнений соответствует прямая 1 – 2 на рисунке, второму уравнению – прямая 3 – 4. Амплитуда результирующего колебания в обоих случаях будет равна.
Амплитуда результирующего колебания в обоих случаях будет равна.
 ,
,  , то уравнение (1) преобразуется к виду
, то уравнение (1) преобразуется к виду .
. и
и  . Полуоси эллипса равны соответствующим амплитудам колебаний. Это случай эллиптически поляризованных колебаний.
. Полуоси эллипса равны соответствующим амплитудам колебаний. Это случай эллиптически поляризованных колебаний.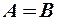 эллипс вырождается в окружность. Это циркулярно поляризованные колебания.
эллипс вырождается в окружность. Это циркулярно поляризованные колебания.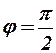 . Уравнения колебаний имеют вид:
. Уравнения колебаний имеют вид:
 ,
, 



