Среди различных колебательных систем особое место занимают электромагнитные (электрические) колебательные системы, при которых электрические величины (токи, заряды) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей. Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур. Рассмотрим подробнее процессы в колебательном контуре.
 Колебательный контур – это электрическая цепь, состоящая из включенных последовательно катушки индуктивностью
Колебательный контур – это электрическая цепь, состоящая из включенных последовательно катушки индуктивностью  , конденсатора емкостью
, конденсатора емкостью  и резистора сопротивлением
и резистора сопротивлением  .
.
Для выяснения механизма возникновения электрических колебаний рассмотрим идеализированный контур, сопротивление которого пренебрежимо мало ( ). Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряды
). Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряды  . В момент времени
. В момент времени  между обкладками конденсатора возникает электрическое поле, энергия которого равна
между обкладками конденсатора возникает электрическое поле, энергия которого равна  . Вся энергия колебательного контура сосредоточена в конденсаторе. Если теперь замкнуть конденсатор на катушку индуктивности, то в контуре потечет возрастающий со временем ток
. Вся энергия колебательного контура сосредоточена в конденсаторе. Если теперь замкнуть конденсатор на катушку индуктивности, то в контуре потечет возрастающий со временем ток  . Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки. Этот процесс закончится, когда конденсатор полностью разрядится, а ток в цепи достигнет максимума. Вся энергия колебательного контура сосредоточена в магнитном поле катушки и равна
. Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки. Этот процесс закончится, когда конденсатор полностью разрядится, а ток в цепи достигнет максимума. Вся энергия колебательного контура сосредоточена в магнитном поле катушки и равна  . С этого момента ток, не меняя направления, начнет убывать. Однако он прекратится не сразу – его будет поддерживать э.д.с. самоиндукции. Ток будет перезаряжать конденсатор, возникнет электрическое поле, стремящееся ослабить ток. Наконец, ток прекратится, а заряд на пластинах конденсатора достигнет максимума. С этого момента конденсатор начнет вновь разряжаться, ток потечет в обратном направлении и процесс повторится.
. С этого момента ток, не меняя направления, начнет убывать. Однако он прекратится не сразу – его будет поддерживать э.д.с. самоиндукции. Ток будет перезаряжать конденсатор, возникнет электрическое поле, стремящееся ослабить ток. Наконец, ток прекратится, а заряд на пластинах конденсатора достигнет максимума. С этого момента конденсатор начнет вновь разряжаться, ток потечет в обратном направлении и процесс повторится.
 Поскольку мы предполагаем, что потерь энергии нет, в контуре будут совершаться периодические незатухающие колебания: периодически будет изменяться заряд на обкладках конденсатора, напряжение на конденсаторе и сила тока, текущего через катушку индуктивности. Следовательно, в контуре возникают электрические колебания, которые сопровождаются превращениями энергии электрического и магнитного полей. Стадии этого процесса более подробно показаны в таблице. В этой же таблице электрические колебания контура сопоставляются с механическими колебаниями маятника. Видна аналогия между массой и индуктивностью, и между коэффициентом жёсткости пружины и величиной обратной ёмкости конденсатора.
Поскольку мы предполагаем, что потерь энергии нет, в контуре будут совершаться периодические незатухающие колебания: периодически будет изменяться заряд на обкладках конденсатора, напряжение на конденсаторе и сила тока, текущего через катушку индуктивности. Следовательно, в контуре возникают электрические колебания, которые сопровождаются превращениями энергии электрического и магнитного полей. Стадии этого процесса более подробно показаны в таблице. В этой же таблице электрические колебания контура сопоставляются с механическими колебаниями маятника. Видна аналогия между массой и индуктивностью, и между коэффициентом жёсткости пружины и величиной обратной ёмкости конденсатора.
Найдем уравнение колебаний в контуре без активного сопротивления. Будем искать закон изменения заряда на обкладках конденсатора. Пусть положительным будет такое направление тока в контуре, когда конденсатор заряжается. Сила тока в цепи определяется выражением
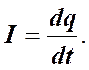
Рассмотрим цепь 1 – 3 – 2 и запишем для нее закон Ома в общем виде для неоднородного участка цепи:
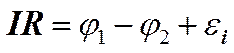
ei – э.д.с., действующая на участке цепи 1 – 2.
Или 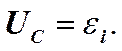
э.д.с. положительна, т.к. способствует движению положительно заряженных носителей тока в выбранном направлении. В рассматриваемом случае  ,
,  ,
,  . Подставим эти значения в выражение для закона Ома, получим:
. Подставим эти значения в выражение для закона Ома, получим:
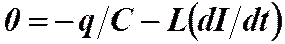
Перепишем  через заряд (
через заряд ( ), получим
), получим

Если ввести обозначение  , получим выражение вида
, получим выражение вида
 ,
,


которое представляет дифференциальное уравнение гармонических колебаний в контуре и подобно соответствующим уравнениям механических колебаний. Решением этого уравнения является выражение
 .
.
Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой, определяемой параметрами контура  и
и  . Эта частота называется собственной частотой контура и соответствует собственной частоте гармонического осциллятора. Выражение для периода колебаний называется формулой Томсона:
. Эта частота называется собственной частотой контура и соответствует собственной частоте гармонического осциллятора. Выражение для периода колебаний называется формулой Томсона:
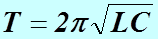
Запишем формулу для напряжения на конденсаторе:
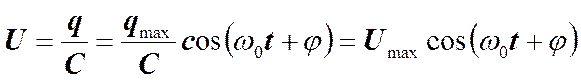
Получим выражение для тока в контуре, продифференцировав соотношение для заряда:
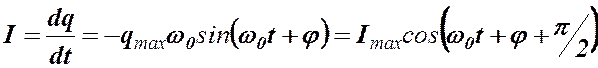
Таким образом, сила тока опережает по фазе напряжение на конденсаторе на  . Сопоставление полученных для заряда, напряжения на конденсаторе и тока в контуре выражений показывает, что в момент, когда ток достигает наибольшего значения, заряд и напряжение обращаются в нуль и наоборот.
. Сопоставление полученных для заряда, напряжения на конденсаторе и тока в контуре выражений показывает, что в момент, когда ток достигает наибольшего значения, заряд и напряжение обращаются в нуль и наоборот.
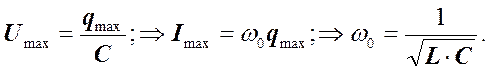
Тогда можно записать.
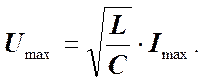
 – это волновое сопротивление (измеряется в Ом).
– это волновое сопротивление (измеряется в Ом).

 Колебательный контур – это электрическая цепь, состоящая из включенных последовательно катушки индуктивностью
Колебательный контур – это электрическая цепь, состоящая из включенных последовательно катушки индуктивностью  , конденсатора емкостью
, конденсатора емкостью  и резистора сопротивлением
и резистора сопротивлением  .
. ). Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряды
). Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряды  . В момент времени
. В момент времени  между обкладками конденсатора возникает электрическое поле, энергия которого равна
между обкладками конденсатора возникает электрическое поле, энергия которого равна  . Вся энергия колебательного контура сосредоточена в конденсаторе. Если теперь замкнуть конденсатор на катушку индуктивности, то в контуре потечет возрастающий со временем ток
. Вся энергия колебательного контура сосредоточена в конденсаторе. Если теперь замкнуть конденсатор на катушку индуктивности, то в контуре потечет возрастающий со временем ток  . Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки. Этот процесс закончится, когда конденсатор полностью разрядится, а ток в цепи достигнет максимума. Вся энергия колебательного контура сосредоточена в магнитном поле катушки и равна
. Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки. Этот процесс закончится, когда конденсатор полностью разрядится, а ток в цепи достигнет максимума. Вся энергия колебательного контура сосредоточена в магнитном поле катушки и равна  . С этого момента ток, не меняя направления, начнет убывать. Однако он прекратится не сразу – его будет поддерживать э.д.с. самоиндукции. Ток будет перезаряжать конденсатор, возникнет электрическое поле, стремящееся ослабить ток. Наконец, ток прекратится, а заряд на пластинах конденсатора достигнет максимума. С этого момента конденсатор начнет вновь разряжаться, ток потечет в обратном направлении и процесс повторится.
. С этого момента ток, не меняя направления, начнет убывать. Однако он прекратится не сразу – его будет поддерживать э.д.с. самоиндукции. Ток будет перезаряжать конденсатор, возникнет электрическое поле, стремящееся ослабить ток. Наконец, ток прекратится, а заряд на пластинах конденсатора достигнет максимума. С этого момента конденсатор начнет вновь разряжаться, ток потечет в обратном направлении и процесс повторится. Поскольку мы предполагаем, что потерь энергии нет, в контуре будут совершаться периодические незатухающие колебания: периодически будет изменяться заряд на обкладках конденсатора, напряжение на конденсаторе и сила тока, текущего через катушку индуктивности. Следовательно, в контуре возникают электрические колебания, которые сопровождаются превращениями энергии электрического и магнитного полей. Стадии этого процесса более подробно показаны в таблице. В этой же таблице электрические колебания контура сопоставляются с механическими колебаниями маятника. Видна аналогия между массой и индуктивностью, и между коэффициентом жёсткости пружины и величиной обратной ёмкости конденсатора.
Поскольку мы предполагаем, что потерь энергии нет, в контуре будут совершаться периодические незатухающие колебания: периодически будет изменяться заряд на обкладках конденсатора, напряжение на конденсаторе и сила тока, текущего через катушку индуктивности. Следовательно, в контуре возникают электрические колебания, которые сопровождаются превращениями энергии электрического и магнитного полей. Стадии этого процесса более подробно показаны в таблице. В этой же таблице электрические колебания контура сопоставляются с механическими колебаниями маятника. Видна аналогия между массой и индуктивностью, и между коэффициентом жёсткости пружины и величиной обратной ёмкости конденсатора.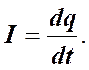
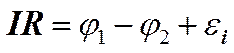
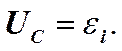
 ,
,  ,
,  . Подставим эти значения в выражение для закона Ома, получим:
. Подставим эти значения в выражение для закона Ома, получим: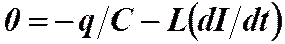
 через заряд (
через заряд ( ), получим
), получим
 , получим выражение вида
, получим выражение вида ,
,

 .
. и
и  . Эта частота называется собственной частотой контура и соответствует собственной частоте гармонического осциллятора. Выражение для периода колебаний называется формулой Томсона:
. Эта частота называется собственной частотой контура и соответствует собственной частоте гармонического осциллятора. Выражение для периода колебаний называется формулой Томсона: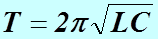
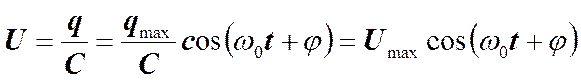
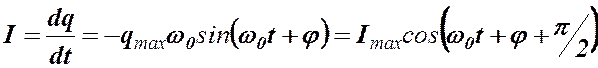
 . Сопоставление полученных для заряда, напряжения на конденсаторе и тока в контуре выражений показывает, что в момент, когда ток достигает наибольшего значения, заряд и напряжение обращаются в нуль и наоборот.
. Сопоставление полученных для заряда, напряжения на конденсаторе и тока в контуре выражений показывает, что в момент, когда ток достигает наибольшего значения, заряд и напряжение обращаются в нуль и наоборот.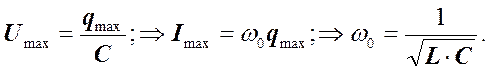
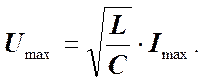
 – это волновое сопротивление (измеряется в Ом).
– это волновое сопротивление (измеряется в Ом).


