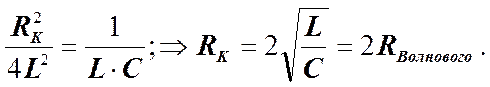Реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постепенно расходуется на этом сопротивлении на нагревание, вследствие чего свободные колебания затухают. Учтем фактор затухания в выражении для закона Ома или по второму правилу Кирхгофа.
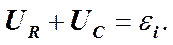
 .
.
 Разделим это уравнение на
Разделим это уравнение на  и заменим ток
и заменим ток  на заряд
на заряд  . В итоге получим:
. В итоге получим:
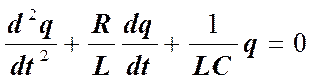
Введем обозначение  и, учитывая, что
и, учитывая, что  , получим окончательно.
, получим окончательно.

Это уравнение, как и ожидалось, совпадает с дифференциальным уравнением затухающих механических колебаний. При условии, что 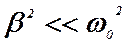 , т.е. при
, т.е. при  решение уравнения затухающих колебаний имеет вид
решение уравнения затухающих колебаний имеет вид
 , (1)
, (1)
где  . Если в это выражение подставить соответствующие выражения для
. Если в это выражение подставить соответствующие выражения для  и
и  , получим следующее соотношение для частоты затухающих колебаний:
, получим следующее соотношение для частоты затухающих колебаний:
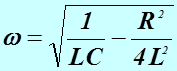
При  получится выражение для собственной частоты незатухающих свободных колебаний в контуре.
получится выражение для собственной частоты незатухающих свободных колебаний в контуре.
Из уравнения для затухающих колебаний легко получить формулу для напряжения на конденсаторе, разделив уравнение (1) на емкость 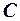 , и выражение для тока в контуре после дифференцирования этого же уравнения. Отпуская эти и ряд других несложных преобразований, запишем лишь один из результатов анализа формул, которые после этих преобразований могут быть получены. Этот результат касается разности фаз между током и падением напряжения на конденсаторе колебательного контура: при наличии активного сопротивления в контуре сила тока опережает по фазе напряжение на конденсаторе на угол
, и выражение для тока в контуре после дифференцирования этого же уравнения. Отпуская эти и ряд других несложных преобразований, запишем лишь один из результатов анализа формул, которые после этих преобразований могут быть получены. Этот результат касается разности фаз между током и падением напряжения на конденсаторе колебательного контура: при наличии активного сопротивления в контуре сила тока опережает по фазе напряжение на конденсаторе на угол  , больший, чем
, больший, чем  (
( ).
).
График изменения заряда со временем изображен на рисунке и подобен соответствующему графику для механических колебаний.
Как и в случае механических колебаний, затухание электрических колебаний характеризуется логарифмическим декрементом затухания:
 .
.
 Логарифмический декремент затухания обратен по величине числу колебаний
Логарифмический декремент затухания обратен по величине числу колебаний  , совершаемых за время, в течение которого амплитуда затухающего колебания уменьшится в
, совершаемых за время, в течение которого амплитуда затухающего колебания уменьшится в  раз (за время релаксации). Если в выражение для логарифмического декремента затухания
раз (за время релаксации). Если в выражение для логарифмического декремента затухания  подставить значения для
подставить значения для  и
и 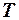 , получим следующую форму записи:
, получим следующую форму записи:
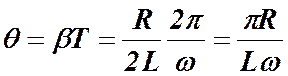
Получили, что логарифмический декремент затухания определяется параметрами контура, т.е. является его характеристикой.
Добротность контура – это величина, обратно пропорциональная логарифмическому декременту затухания.
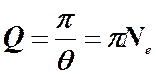
Добротность контура пропорциональна числу колебаний  , совершаемых за время релаксации. Добротность тем выше, чем большее число колебаний успевает совершиться прежде, чем амплитуда уменьшится в
, совершаемых за время релаксации. Добротность тем выше, чем большее число колебаний успевает совершиться прежде, чем амплитуда уменьшится в 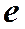 раз.
раз.
Добротность контура определяется ещё и по-другому.

 Это отношение энергии в контуре в данный момент времени к убыли энергии за один период, следующий за этим моментом.
Это отношение энергии в контуре в данный момент времени к убыли энергии за один период, следующий за этим моментом.
При 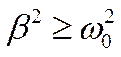 , т.е. при
, т.е. при  происходит апериодический разряд.
происходит апериодический разряд.
Конденсатор просто разряжается на сопротивление, и колебания не происходят.
Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим сопротивлением.
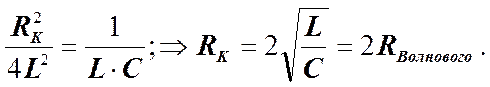

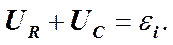
 .
. Разделим это уравнение на
Разделим это уравнение на  и заменим ток
и заменим ток  на заряд
на заряд  . В итоге получим:
. В итоге получим: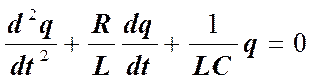
 и, учитывая, что
и, учитывая, что  , получим окончательно.
, получим окончательно.
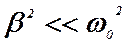 , т.е. при
, т.е. при  решение уравнения затухающих колебаний имеет вид
решение уравнения затухающих колебаний имеет вид , (1)
, (1) . Если в это выражение подставить соответствующие выражения для
. Если в это выражение подставить соответствующие выражения для  и
и  , получим следующее соотношение для частоты затухающих колебаний:
, получим следующее соотношение для частоты затухающих колебаний: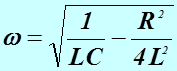
 получится выражение для собственной частоты незатухающих свободных колебаний в контуре.
получится выражение для собственной частоты незатухающих свободных колебаний в контуре.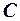 , и выражение для тока в контуре после дифференцирования этого же уравнения. Отпуская эти и ряд других несложных преобразований, запишем лишь один из результатов анализа формул, которые после этих преобразований могут быть получены. Этот результат касается разности фаз между током и падением напряжения на конденсаторе колебательного контура: при наличии активного сопротивления в контуре сила тока опережает по фазе напряжение на конденсаторе на угол
, и выражение для тока в контуре после дифференцирования этого же уравнения. Отпуская эти и ряд других несложных преобразований, запишем лишь один из результатов анализа формул, которые после этих преобразований могут быть получены. Этот результат касается разности фаз между током и падением напряжения на конденсаторе колебательного контура: при наличии активного сопротивления в контуре сила тока опережает по фазе напряжение на конденсаторе на угол  , больший, чем
, больший, чем  (
( ).
). .
. Логарифмический декремент затухания обратен по величине числу колебаний
Логарифмический декремент затухания обратен по величине числу колебаний  , совершаемых за время, в течение которого амплитуда затухающего колебания уменьшится в
, совершаемых за время, в течение которого амплитуда затухающего колебания уменьшится в  раз (за время релаксации). Если в выражение для логарифмического декремента затухания
раз (за время релаксации). Если в выражение для логарифмического декремента затухания  подставить значения для
подставить значения для 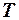 , получим следующую форму записи:
, получим следующую форму записи: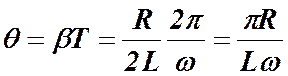
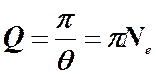
 , совершаемых за время релаксации. Добротность тем выше, чем большее число колебаний успевает совершиться прежде, чем амплитуда уменьшится в
, совершаемых за время релаксации. Добротность тем выше, чем большее число колебаний успевает совершиться прежде, чем амплитуда уменьшится в 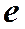 раз.
раз.
 Это отношение энергии в контуре в данный момент времени к убыли энергии за один период, следующий за этим моментом.
Это отношение энергии в контуре в данный момент времени к убыли энергии за один период, следующий за этим моментом.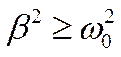 , т.е. при
, т.е. при  происходит апериодический разряд.
происходит апериодический разряд.