Вынужденные механические колебания
Большой интерес для техники представляет возможность поддерживать колебания незатухающими. Для этого необходимо восполнять потери реальной колебательной системы. Восполнение потерь возможно с помощью какого–либо периодически действующего фактора. Пусть таким фактором в механической колебательной системе будет действие вынуждающей силы, изменяющейся по гармоническому закону:
где Рассмотрим пружинный маятник. Уравнение движения такого маятника получено нами в виде:
Приблизим идеализированную колебательную систему к реальной, введя фактор диссипации энергии (потери энергии), например, силы трения. Сила трения пропорциональна скорости, следовательно, выражение для силы трения можно записать.
где Учтем наличие сил трения в законе движения маятника.
Это уравнение свободных затухающих колебаний пружинного маятника. Пусть потери, возникающие в колебательной системе за счет действия сил трения, компенсируются действием вынуждающей силы
Преобразуем это выражение. Разделим обе части на
В итоге получим:
или или Это линейное неоднородное дифференциальное уравнение вынужденных колебаний пружинного маятника. Графически вынужденные колебания изображены на рисунке.
и соответствует свободным затухающим колебаниям. Это решение играет заметную роль только в начальной стадии процесса, при установлении колебаний. С течением времени из-за множителя
Наша задача найти амплитуду вынужденных колебаний A и начальную фазу j вынужденных колебаний. Обратим внимание на то, что скорость опережает смещение на p/2, а ускорение на эту же величину опережает скорость и Распишем смещение, скорость и ускорение через косинус. Выражение (2) примет вид.
Подставим (2'), (3) и (4) в (1).
Разделим всё на амплитуду A.
Каждое слагаемое можно представить в виде соответствующего вращающегося вектора амплитуды.
Решать будем с помощью метода векторных диаграмм.
Из рисунка видно.
Тогда получим.
С учётом (5) окончательно имеем.
При постоянных значениях F0, m и b – амплитуда зависит только от соотношения круговых частот: вынуждающей силы (w) и свободных незатухающих колебаний системы (w0). Начальная фаза вынужденных колебаний определится следующим образом.
Таким образом, установившиеся вынужденные колебания представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Для рассматриваемой колебательной системы с заданными параметрами ( Проанализируем выражение (6). 1. w = 0 (частота вынуждающей силы равна нулю).
2. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для системы частоте амплитуда колебаний достигает максимального значения. Колебательная система оказывается наиболее отзывчивой на действие вынуждающей силы именно на этой частоте. Это явление называется резонансом, а соответствующая частота – резонансной частотой. Для определения резонансной частоты нужно найти минимум выражения, стоящего в знаменателе соотношения для амплитуды вынужденных колебаний. Продифференцируем знаменатель в (6) и приравнять его к нулю, получим выражение для резонансной частоты. Имеем.
Если подставить полученную формулу в выражение для амплитуды вынужденных колебаний в установившемся состоянии, получим выражение для амплитуды при резонансе:
Из этого выражения следует, что при отсутствии сопротивления среды ( b1 < b2 < b Для консервативной системы, т.е. при b = 0 wрез = w0. Для диссипативной системы – wрез несколько меньше собственной круговой частоты (см. выражение 8). С увеличением коэффициента затухания b явление резонанса проявляется всё слабее и исчезает при
Явление резонанса часто оказывается полезным, особенно в акустике, радиотехнике. Вместе с тем, с этим явлением иногда приходится бороться, или, во всяком случае, учитывать. Например, собственная частота вибраций корпуса корабля или крыльев самолета должны сильно отличаться от частоты колебаний, которые могут возбуждаться вращением гребного винта или пропеллера. В противном случае могут возникнуть опасные вибрации, которые могут привести к разрушению.
|

 ,
,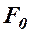 и
и  соответственно амплитуда, и собственная частота вынуждающей силы.
соответственно амплитуда, и собственная частота вынуждающей силы.
 ,
, – коэффициент сопротивления.
– коэффициент сопротивления. .
.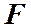 . Тогда уравнение движение маятника можно представить в виде
. Тогда уравнение движение маятника можно представить в виде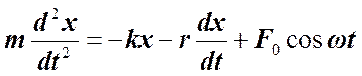 .
. и введем обозначения
и введем обозначения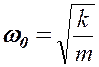 ,
,  – коэффициент затухания пружинного маятника.
– коэффициент затухания пружинного маятника. ,
, , (1)
, (1) .
. В соответствии с правилами математики решение неоднородного дифференциального уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения. Общее решение имеет следующий вид
В соответствии с правилами математики решение неоднородного дифференциального уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения. Общее решение имеет следующий вид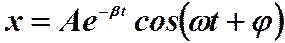
 роль этого слагаемого в общем решении неоднородного дифференциального уравнения уменьшается. По прошествии достаточно большого для установления колебаний промежутка времени им можно пренебречь, сохраняя в решении лишь частное решение неоднородного уравнения. Частное решение, отвечающее установившимся вынужденным колебаниям маятника, может быть получено различными способами и имеет вид:
роль этого слагаемого в общем решении неоднородного дифференциального уравнения уменьшается. По прошествии достаточно большого для установления колебаний промежутка времени им можно пренебречь, сохраняя в решении лишь частное решение неоднородного уравнения. Частное решение, отвечающее установившимся вынужденным колебаниям маятника, может быть получено различными способами и имеет вид: . (2)
. (2)
 (2')
(2') (3)
(3) (4)
(4)


 – амплитуда ускорения.
– амплитуда ускорения. – амплитуда скорости.
– амплитуда скорости.
 – амплитуда смещения.
– амплитуда смещения.
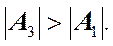




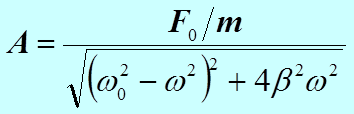 . (6)
. (6) (7)
(7) и
и  ) амплитуда вынужденных колебаний зависит от величины и частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания также зависит от частоты вынуждающей силы.
) амплитуда вынужденных колебаний зависит от величины и частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания также зависит от частоты вынуждающей силы. – это статическая амплитуда, колебания не совершаются.
– это статическая амплитуда, колебания не совершаются. .
.
 Следовательно, равно нулю выражение в скобках.
Следовательно, равно нулю выражение в скобках.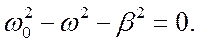 Отсюда получим.
Отсюда получим. . (8)
. (8) .
. ) амплитуда при резонансе обращалась бы в бесконечность. Кроме того, при этом условии резонансная частота совпадает с собственной частотой колебаний системы
) амплитуда при резонансе обращалась бы в бесконечность. Кроме того, при этом условии резонансная частота совпадает с собственной частотой колебаний системы  .
. 3.
3. .
.


