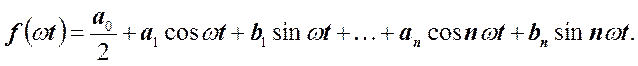Направленных вдоль одной прямой
Пусть точка одновременно участвует в двух гармонических колебаниях одинакового периода, направленных вдоль одной прямой. Сложение колебаний будем производить методом векторных диаграмм. Пусть колебания заданы уравнениями.
Так как колебания совершаются вдоль одной прямой, то и результирующее колебание будет направлено вдоль этой же прямой. Отложим из точки О вектор
Необходимо найти результирующую амплитуду A. Сложение проводим для момента времени t = 0. Вектора отложим под начальными углами j1 и j2. Из рисунка видно, что величину результирующей амплитуды можно получить следующим образом.
Распишем каждое слагаемое.
Учтём.
Перепишем.
Учтём, что косинус отрицательного угла равен косинусу положительного угла, и что j1 < j2. Тогда окончательно запишем.
Начальная фаза результирующего колебания j0 определится из следующего соотношения.
Из анализа выражения (1) для амплитуды следует, что амплитуда A результирующего колебания зависит от разности начальных фаз j2 – j1. Так как разность j2 – j1 = const (такие колебания называются когерентными), то по формуле (1) можно получить вполне определённое значение результирующей амплитуды A. Косинус любого угла заключён в пределах от –1 до +1. Следовательно, возможные значения A лежат в следующих пределах.
Модуль берётся потому, что амплитуда не может быть отрицательной. Рассмотрим для примера несколько случаев. 1. Разность фаз равна нулю или чётному числу p, т.е.
n = 0, ±1, ±2, ±3, …. Тогда cos(j2 – j1) = 1 и A = A1 + A2.
График зависимости смещения от времени будет иметь вид.
2. Разность фаз равна нечётному числу p, т.е.
n = 0, ±1, ±2, ±3, …. Тогда cos(j2 – j1) = – 1 и A =| A1 – A2| = | A2 – A1|. Если A1 = A2, то результирующая амплитуда A = 0, т.е. колебаний не будет.
Из уравнения (1) следует, что результирующая амплитуда A ¹ const, а будет изменяться в соответствии с величиной меняющейся разности фаз исходных колебаний.
Поэтому при сложении некогерентных колебаний не имеет смысла говорить о сложении амплитуд. Следовательно, сумма гармонических колебаний одного направления с разными частотами не является гармоническим колебанием. Но в некоторых случаях наблюдаются вполне определённые закономерности.
Биения
Особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало различаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое колебание называется биениями. Пусть имеются два колебания, различающиеся только частотами:
где Сложив эти колебания и применив теорему сложения косинусов:
получим уравнение результирующего колебания:
В итоге получили выражение для почти гармонического колебания с частотой
Частоту
Периодическое изменение амплитуды от максимума до минимума называются биениями. Амплитуда результирующего колебания изменяется с частотой следующим образом.
Явление биения часто наблюдается при звуковых и электрических колебаниях.
В общем случае колебания вида  называются модулированными. Различают частные случаи: амплитудная модуляция (амплитуда колебания зависит от времени по определённому закону); модуляция по фазе или частоте (фаза колебаний зависит от времени). Биения – это простейший вид модулированных колебаний. называются модулированными. Различают частные случаи: амплитудная модуляция (амплитуда колебания зависит от времени по определённому закону); модуляция по фазе или частоте (фаза колебаний зависит от времени). Биения – это простейший вид модулированных колебаний.
Важной задачей теории колебаний является гармонический анализ, т.е. представление сложных модулированных колебаний в виде суммы (в виде ряда) простых гармонических колебаний. Используются ряды Фурье. Например.
|

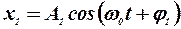 и
и 
 под углом j1 к опорной линии и вектор
под углом j1 к опорной линии и вектор  под углом j1. Оба вектора вращаются против часовой стрелки с одинаковой угловой скоростью w0, поэтому угол j2 – j1 между ними всегда постоянен.
под углом j1. Оба вектора вращаются против часовой стрелки с одинаковой угловой скоростью w0, поэтому угол j2 – j1 между ними всегда постоянен. Нам известно, что проекция суммарного вектора
Нам известно, что проекция суммарного вектора 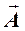 равна сумме проекций слагаемых на эту же ось. Поэтому результирующее колебание может быть изображено вектором амплитуды
равна сумме проекций слагаемых на эту же ось. Поэтому результирующее колебание может быть изображено вектором амплитуды  , вращающимся вокруг точки О с той же угловой скоростью w0, что и вектора
, вращающимся вокруг точки О с той же угловой скоростью w0, что и вектора 
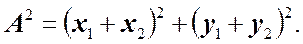









 (1)
(1)
 (2)
(2)







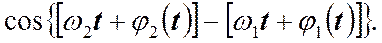
 ,
, ,
, .
. ,
,
 , амплитуда которого изменяется по некоторому периодическому закону.
, амплитуда которого изменяется по некоторому периодическому закону.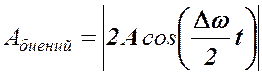
 называют циклической частотой биений.
называют циклической частотой биений. – период биений.
– период биений.