Гармонические колебания и их характеристики
Гармонические колебания представляют собой наиболее простой вид колебаний. Гармоническими называются такие колебания, при которых колеблющаяся величина изменяется со временем по закону косинуса (синуса). Изучение гармонических колебаний важно по следующим причинам: а) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; б) различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение периодических колебаний. Гармонические колебания некоторой величины
где
При Существуют связи между параметрами гармонических колебаний:
где Необходимо отметить, что выражение с синусом используется тогда, когда колебания начинаются от положения равновесия. А выражение с косинусом применяются тогда, когда колебания начинаются от максимального отклонения. Продолжим рассмотрение характеристик свободных гармонических колебаний. Определим скорость и ускорение колеблющейся материальной точки.
Видно, что скорость и ускорение колеблющейся точки изменяются со временем также по гармоническому закону. Колебания скорости опережают колебания координаты на угол Кинетическая энергия К материальной точки массой
Для определения потенциальной энергии П материальной точки, запишем выражение для силы
Поскольку Такая зависимость характерна для упругой силы. Работа этой силы при элементарном бесконечно малом изменении конфигурации системы (изменении
Кинетическая и потенциальная энергии периодически изменяются от 0 до
|

 описываются уравнениями вида:
описываются уравнениями вида: ,
, ,
,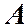 – амплитуда колебания, т.е. положительное наибольшее отклонение величины
– амплитуда колебания, т.е. положительное наибольшее отклонение величины  от ее значения в состоянии равновесия;
от ее значения в состоянии равновесия; – круговая или циклическая частота;
– круговая или циклическая частота; и
и 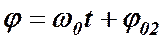 – фазы колебаний, характеризующие текущее отклонение величины
– фазы колебаний, характеризующие текущее отклонение величины  от состояния равновесия.
от состояния равновесия.
 или
или 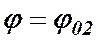 , т.е.
, т.е.  и
и  – это начальные фазы колебаний.
– это начальные фазы колебаний.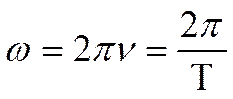 ,
, – частота колебаний или количество полных колебаний в единицу времени,
– частота колебаний или количество полных колебаний в единицу времени,  – период колебаний, или время одного полного колебания.
– период колебаний, или время одного полного колебания. ;
;  ;
;  .
. , колебания ускорения происходят в противофазе с колебаниями координаты (левый рисунок).
, колебания ускорения происходят в противофазе с колебаниями координаты (левый рисунок). , совершающей колебания:
, совершающей колебания:
 , действующей на точку. По второму закону Ньютона
, действующей на точку. По второму закону Ньютона
 ,
,  .
. ) равна приращению потенциальной энергии, взятому со знаком минус:
) равна приращению потенциальной энергии, взятому со знаком минус: .
. по гармоническому закону с частотой
по гармоническому закону с частотой  (правый рисунок). Колебания кинетической энергии происходят в противофазе с колебаниями потенциальной энергии, а их сумма в любой момент времени одинакова (упругая сила консервативна, следовательно, выполняется закон сохранения энергии).
(правый рисунок). Колебания кинетической энергии происходят в противофазе с колебаниями потенциальной энергии, а их сумма в любой момент времени одинакова (упругая сила консервативна, следовательно, выполняется закон сохранения энергии).




